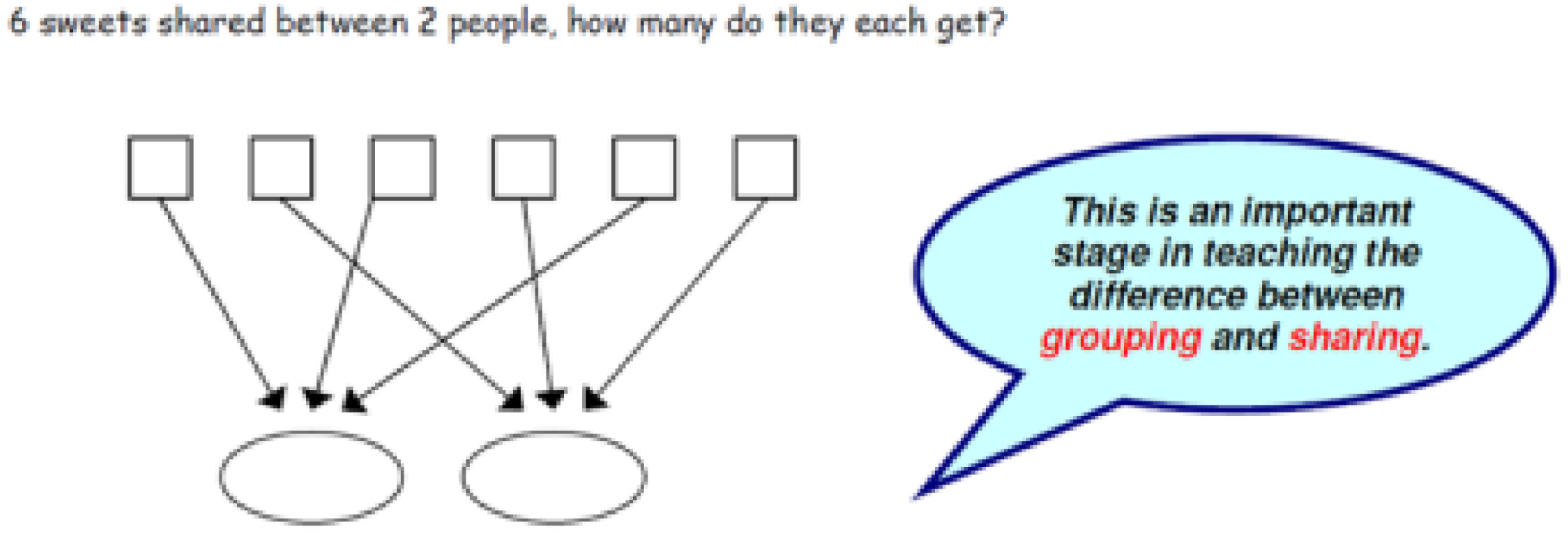
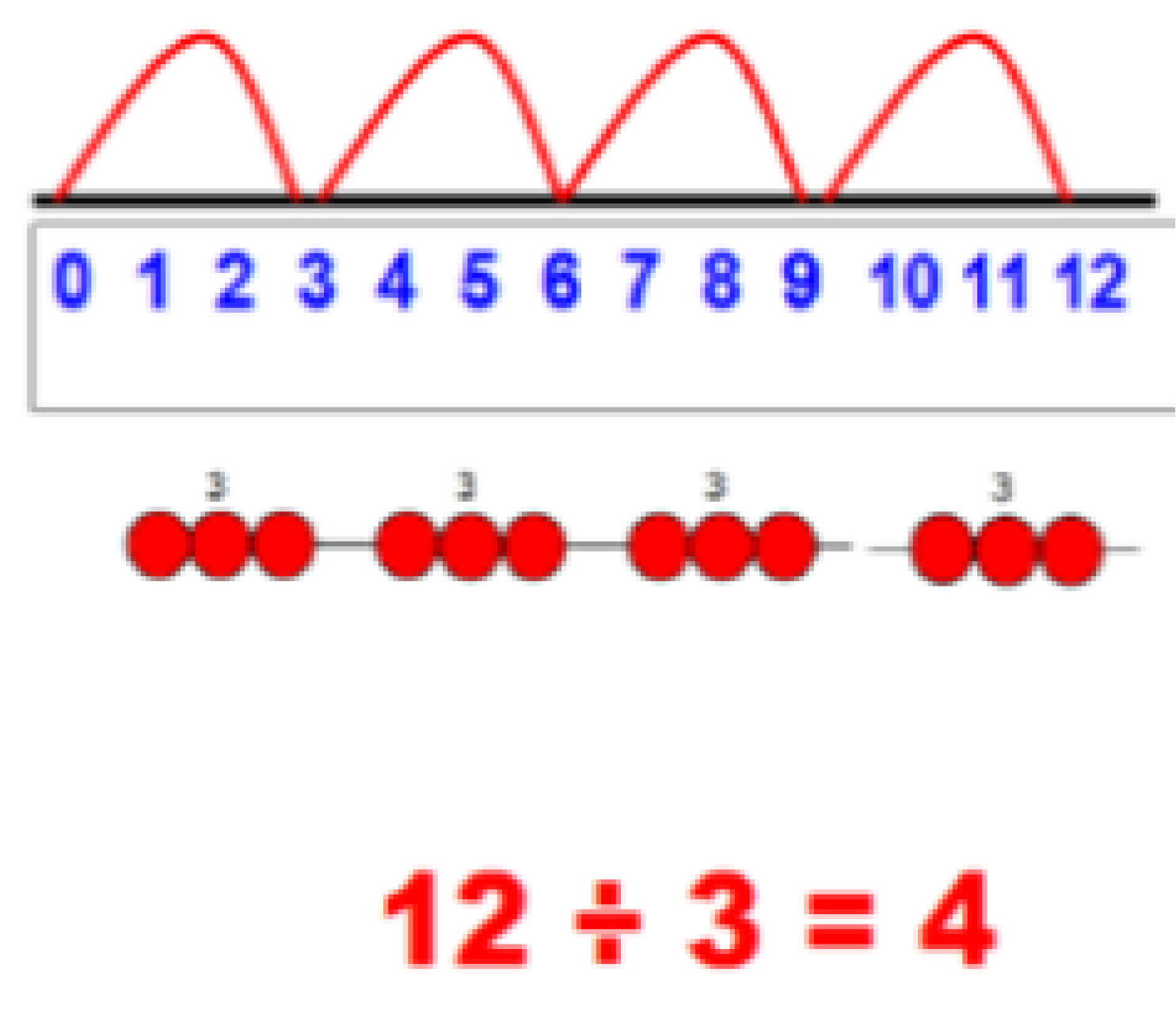
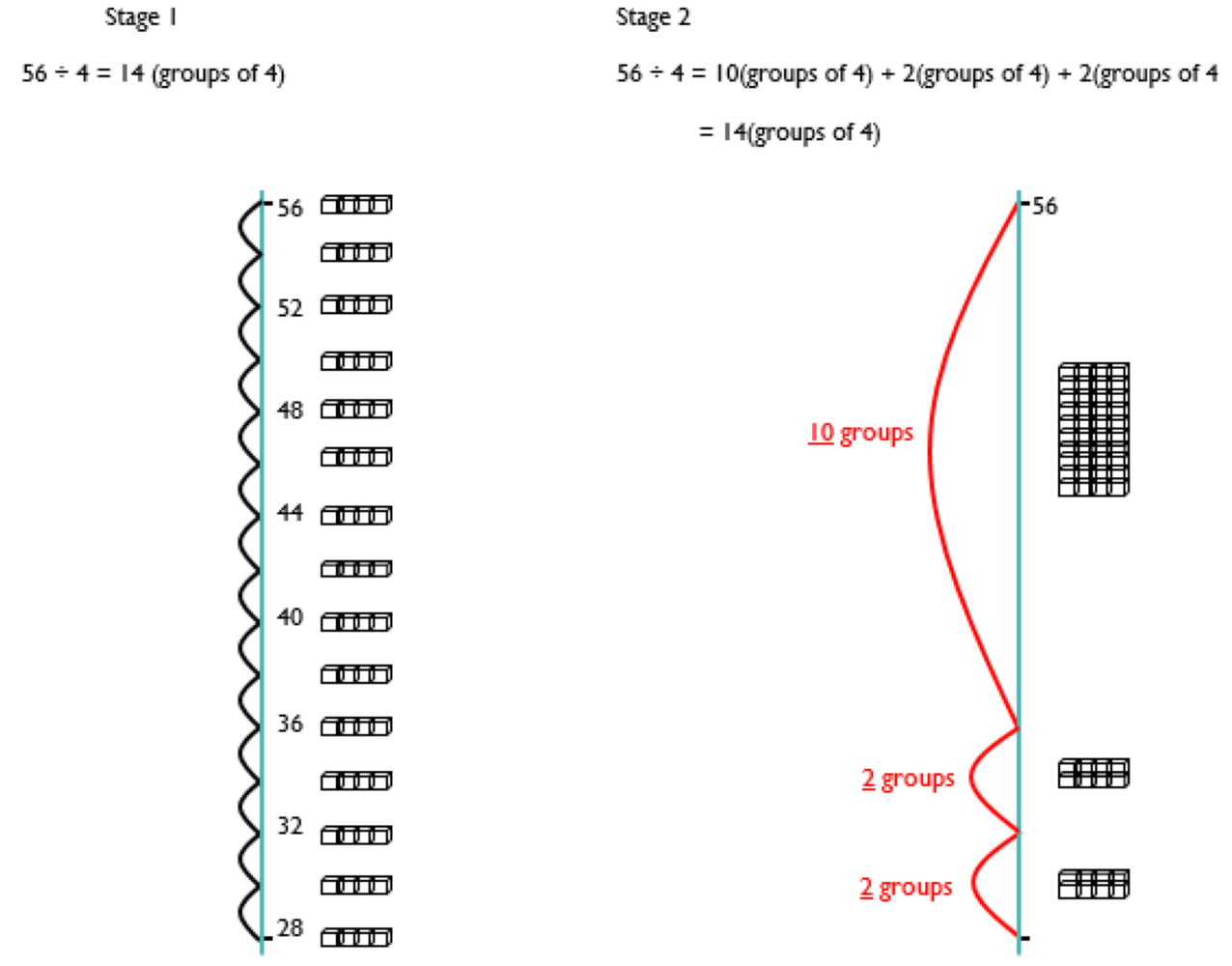
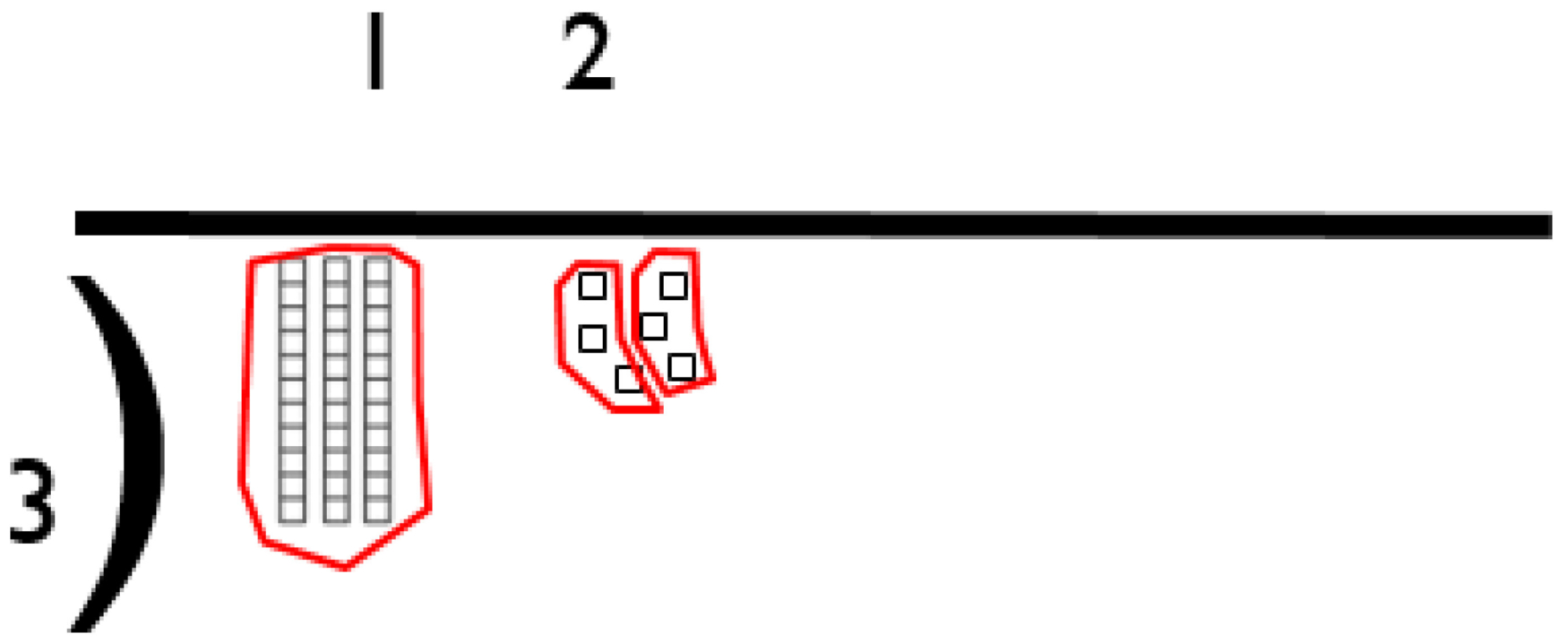
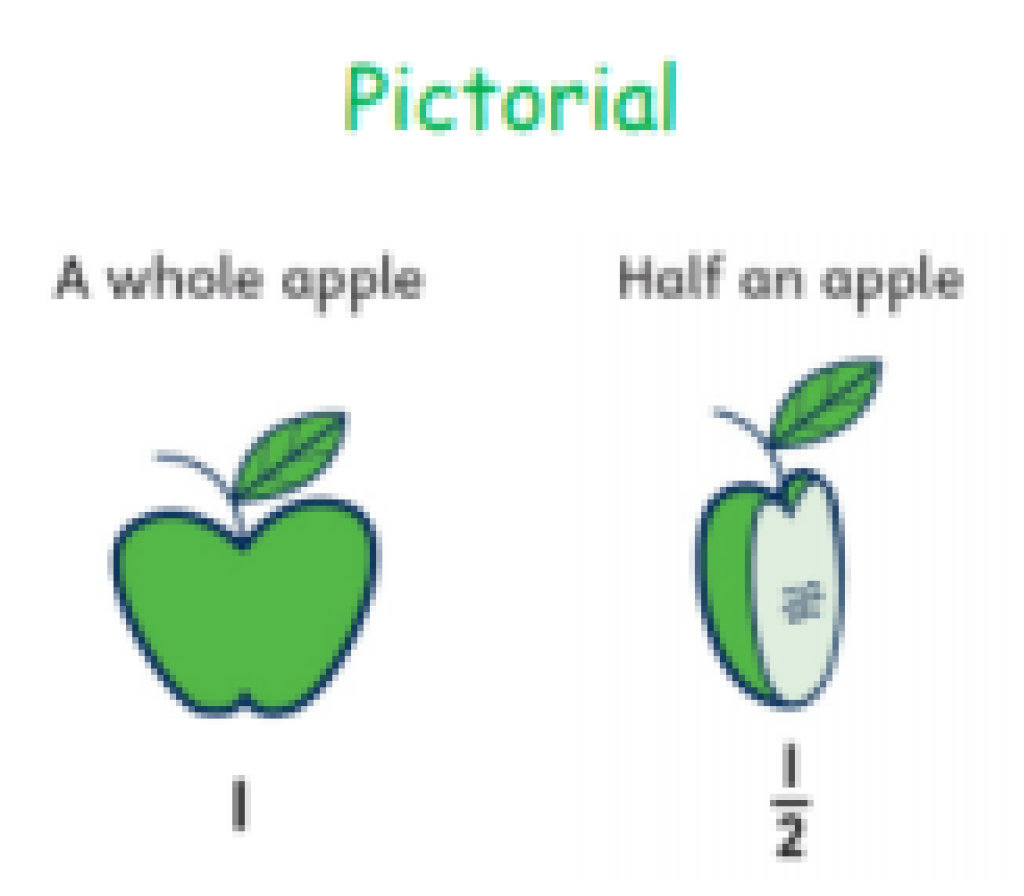
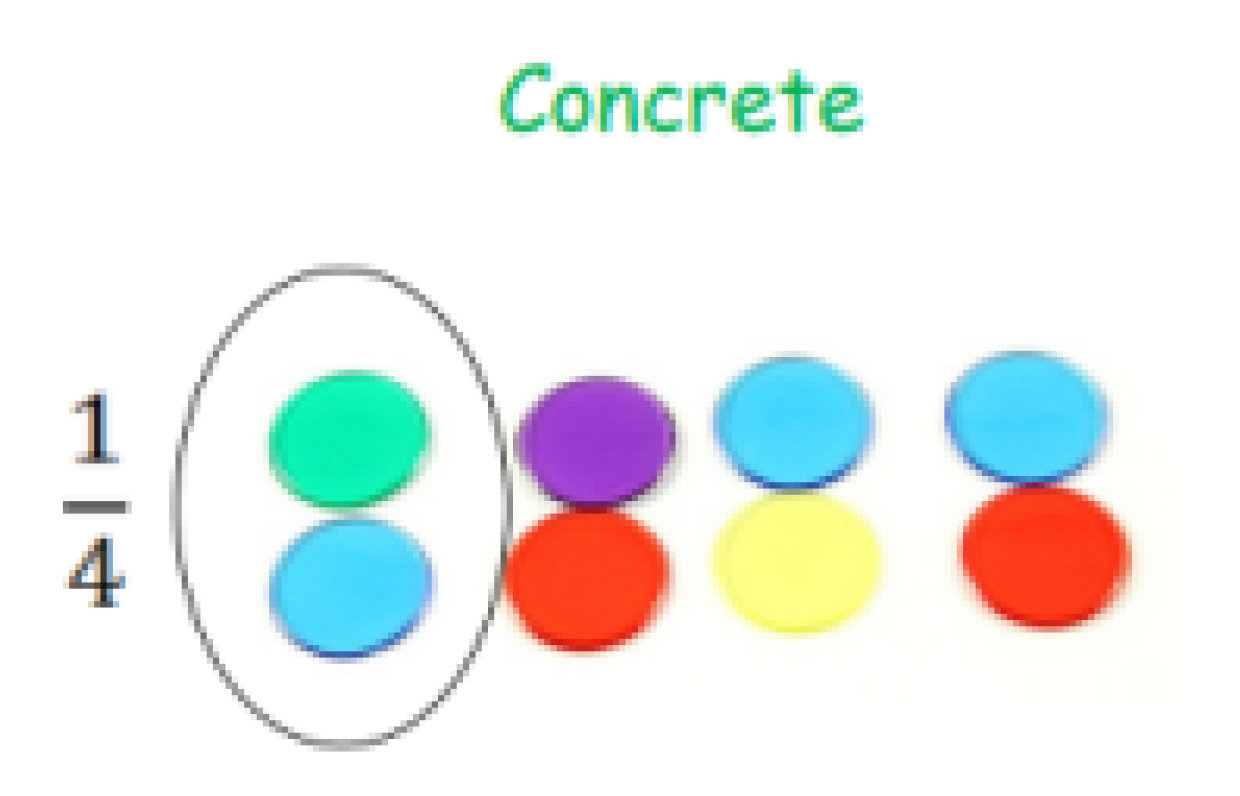
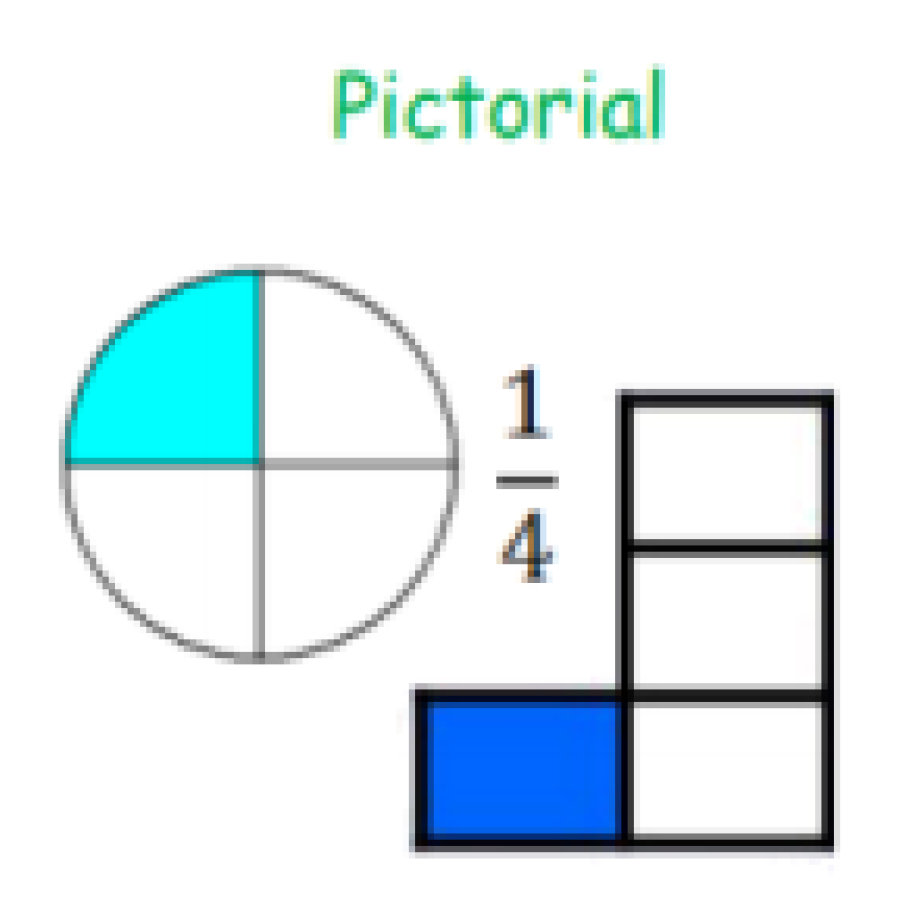
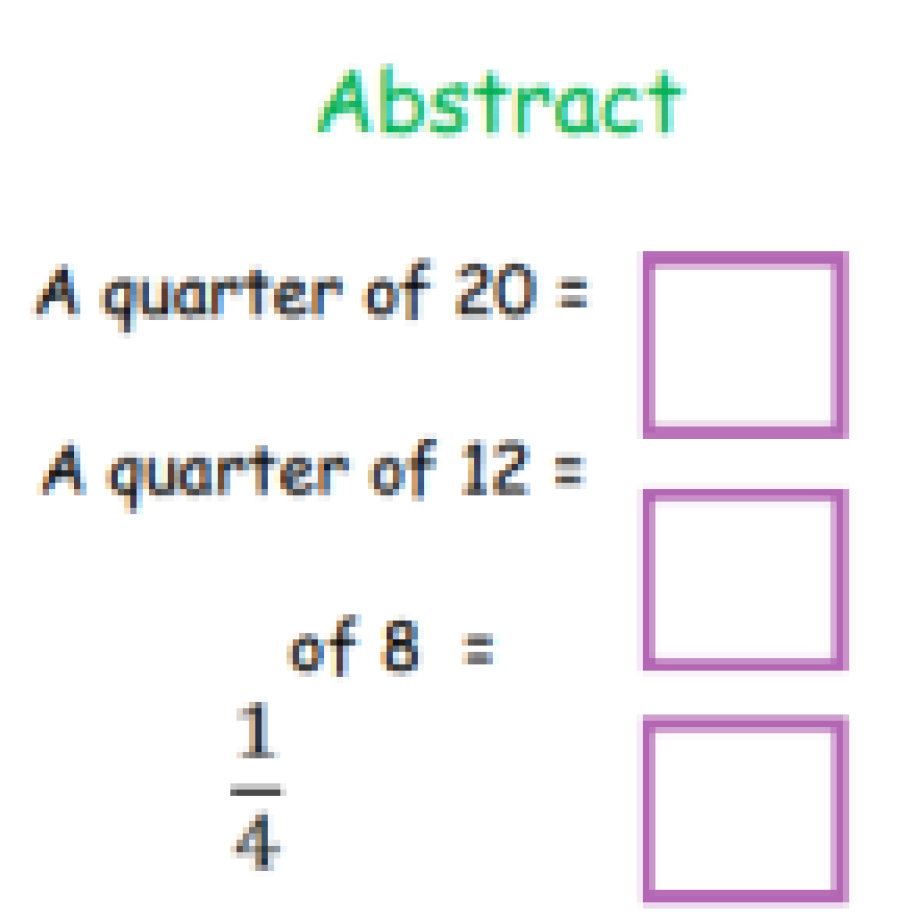
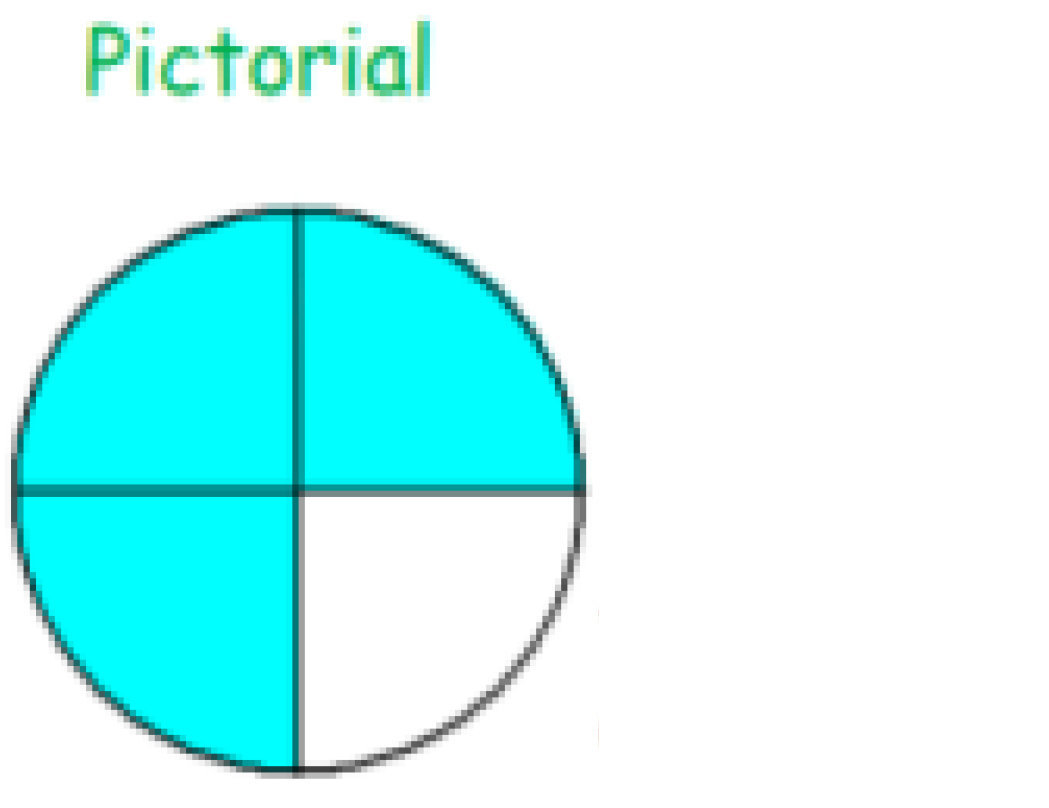
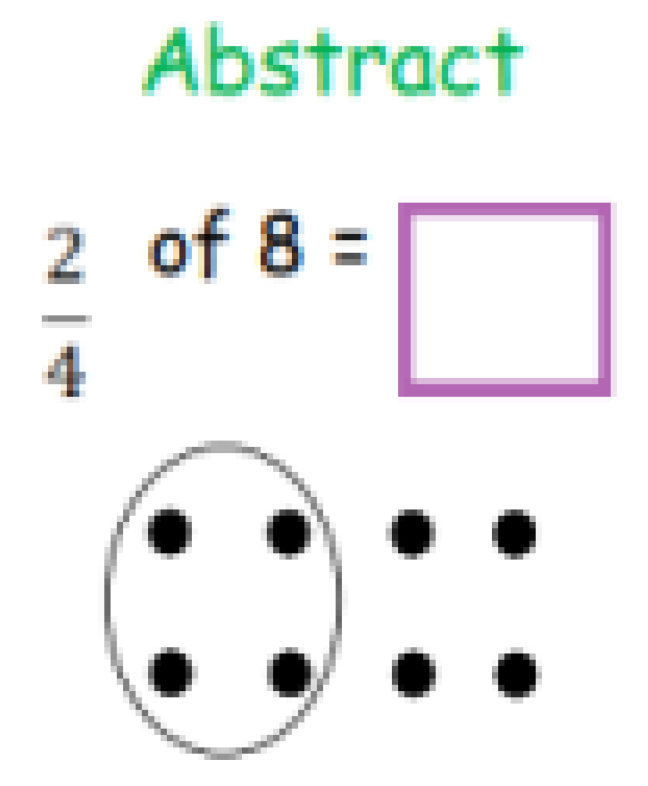
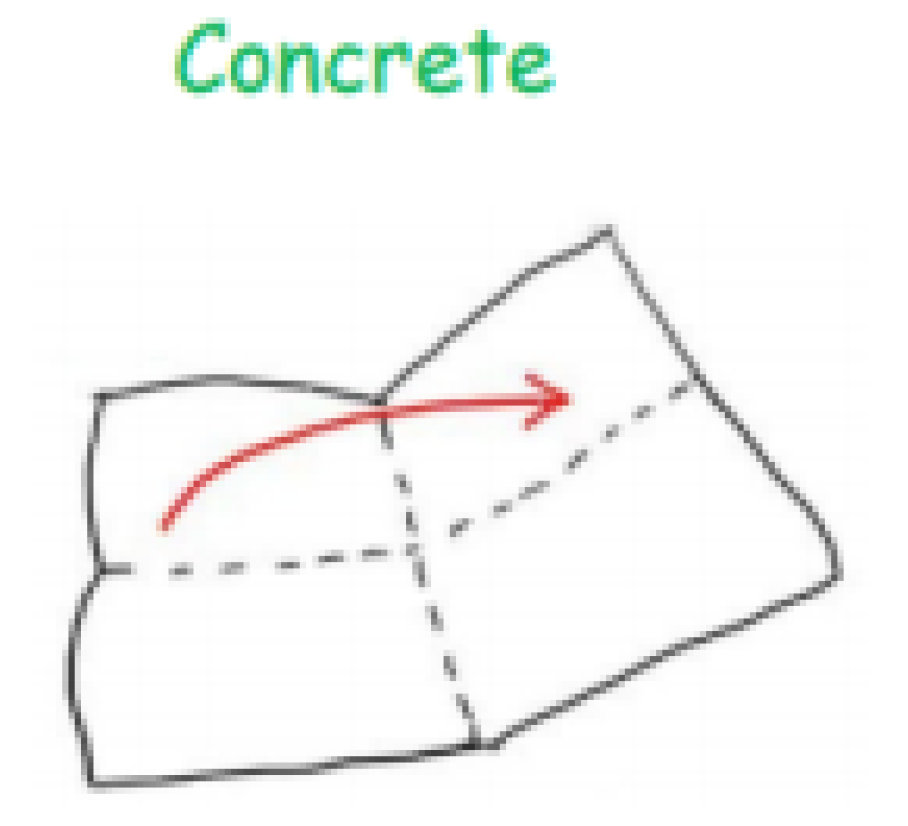
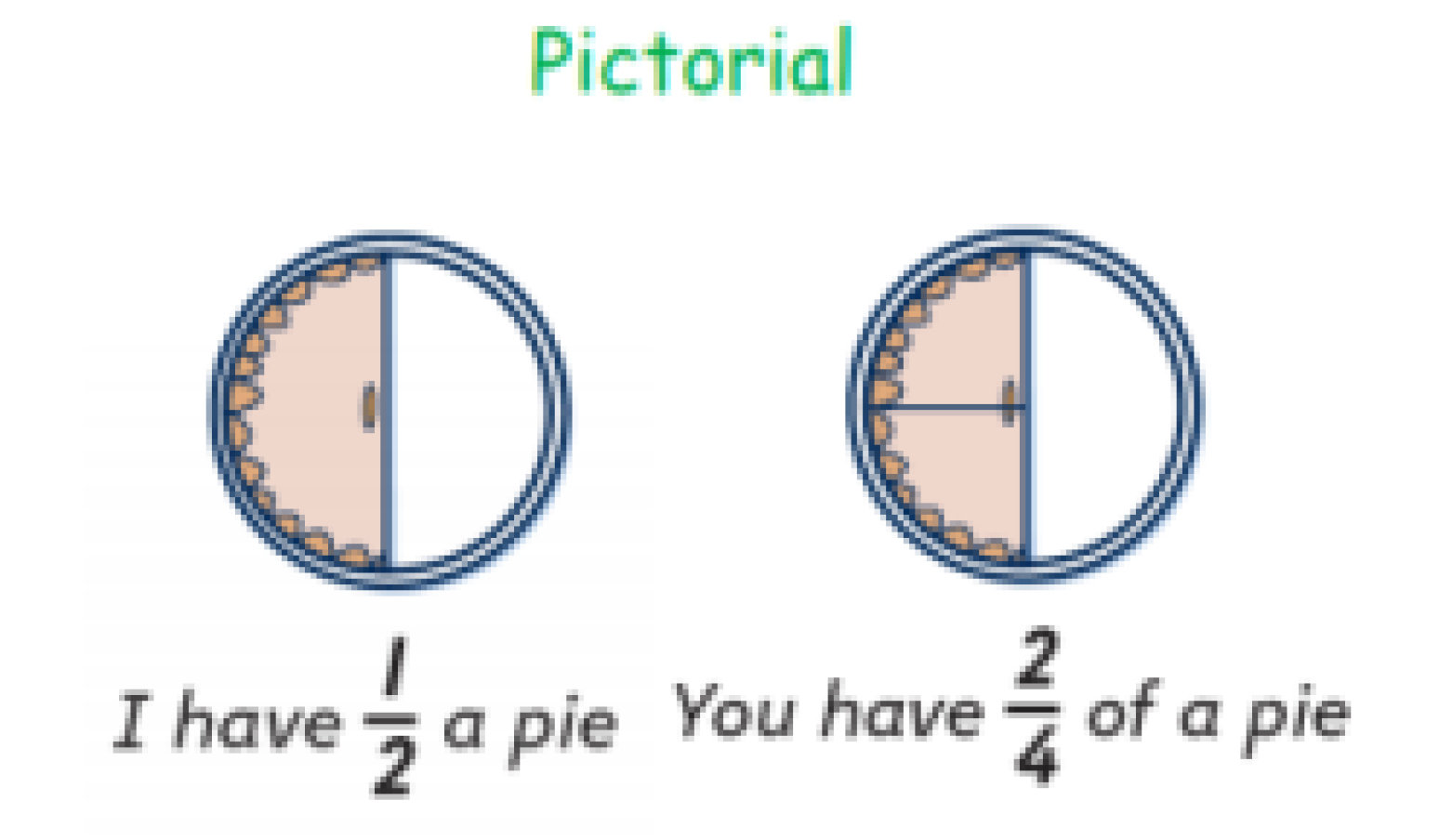
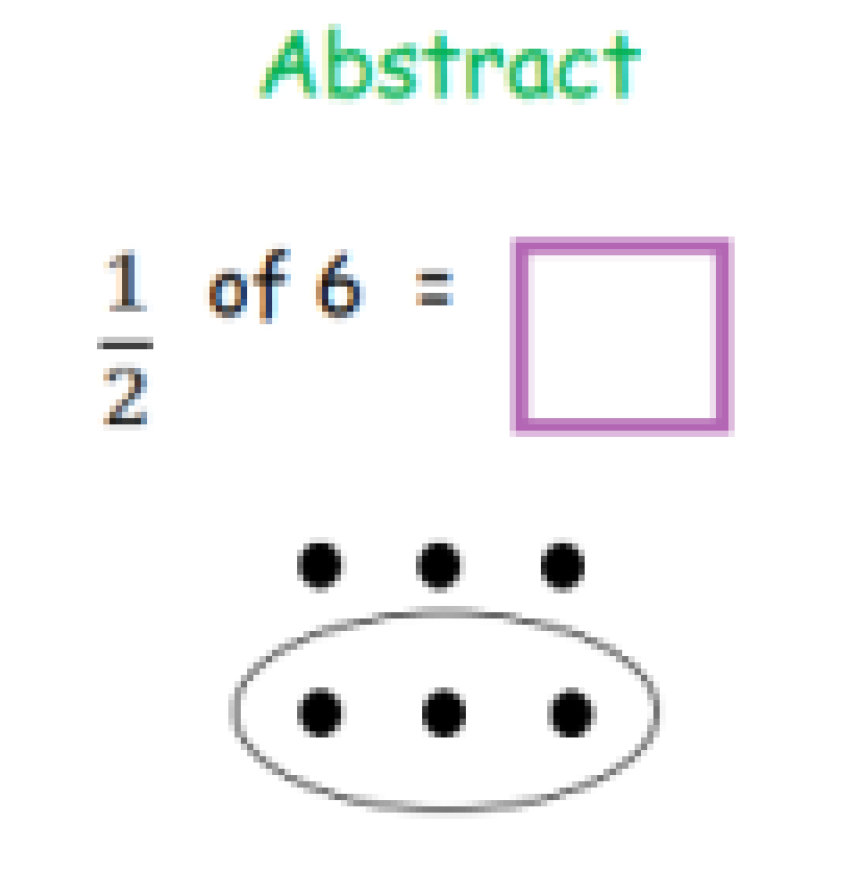
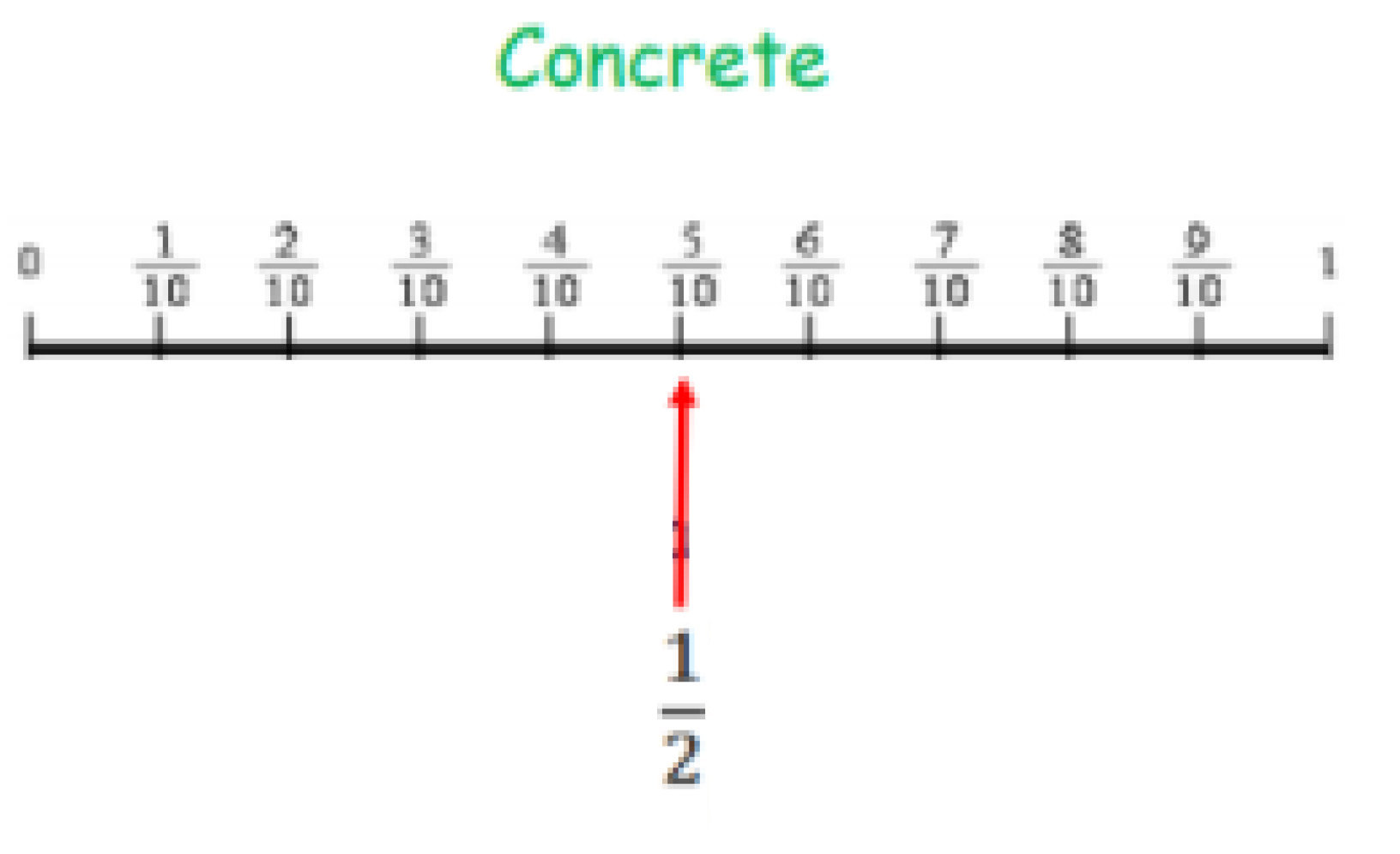
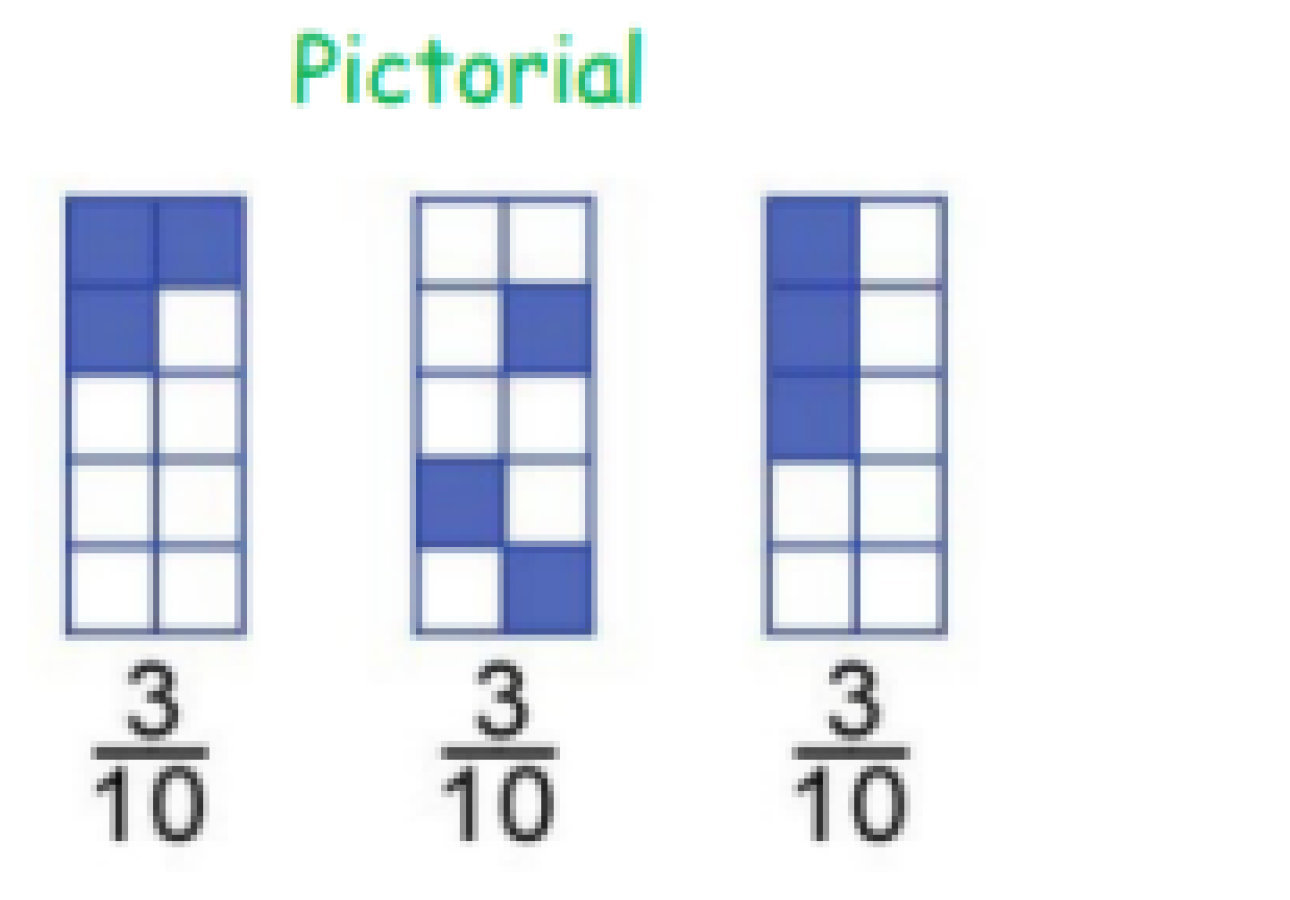
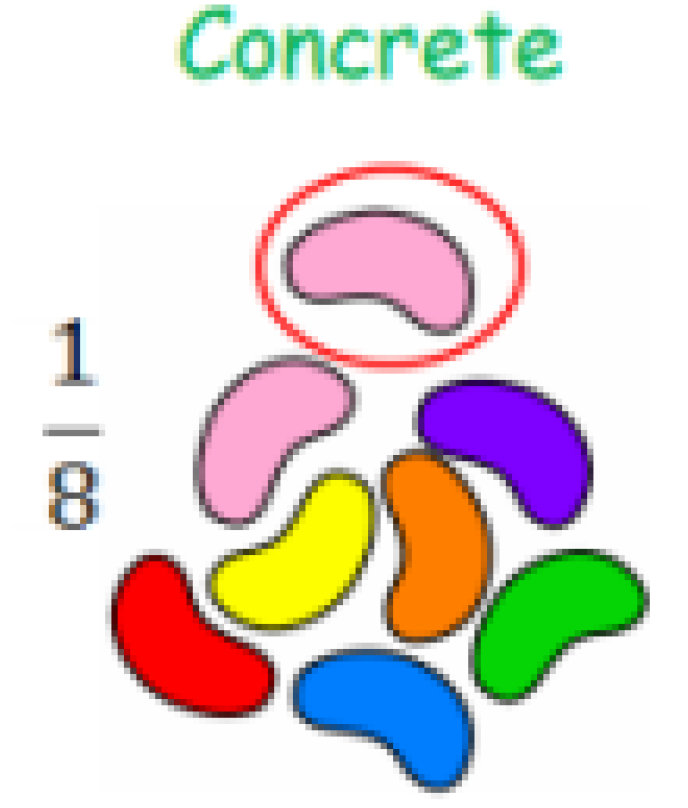
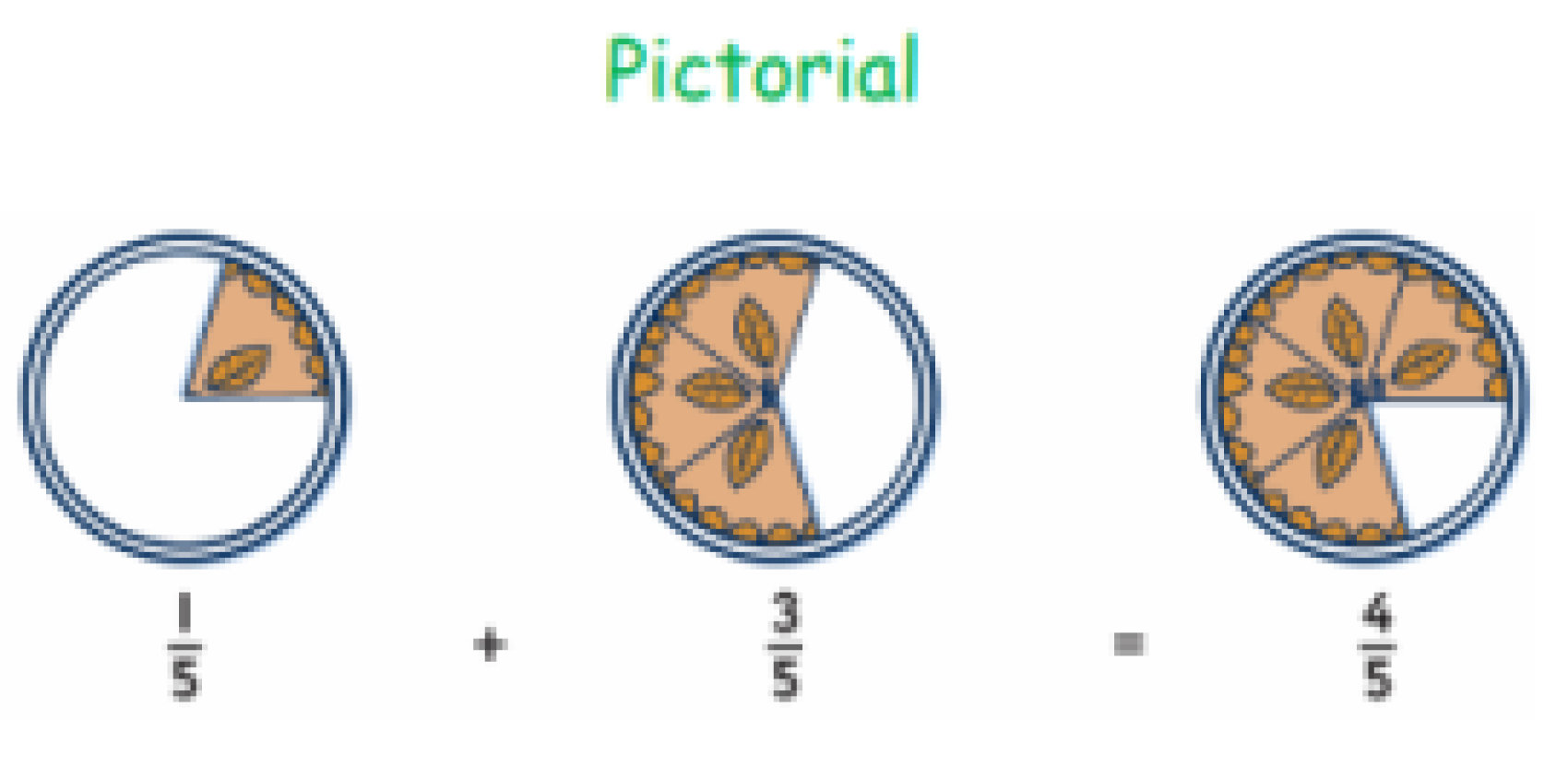
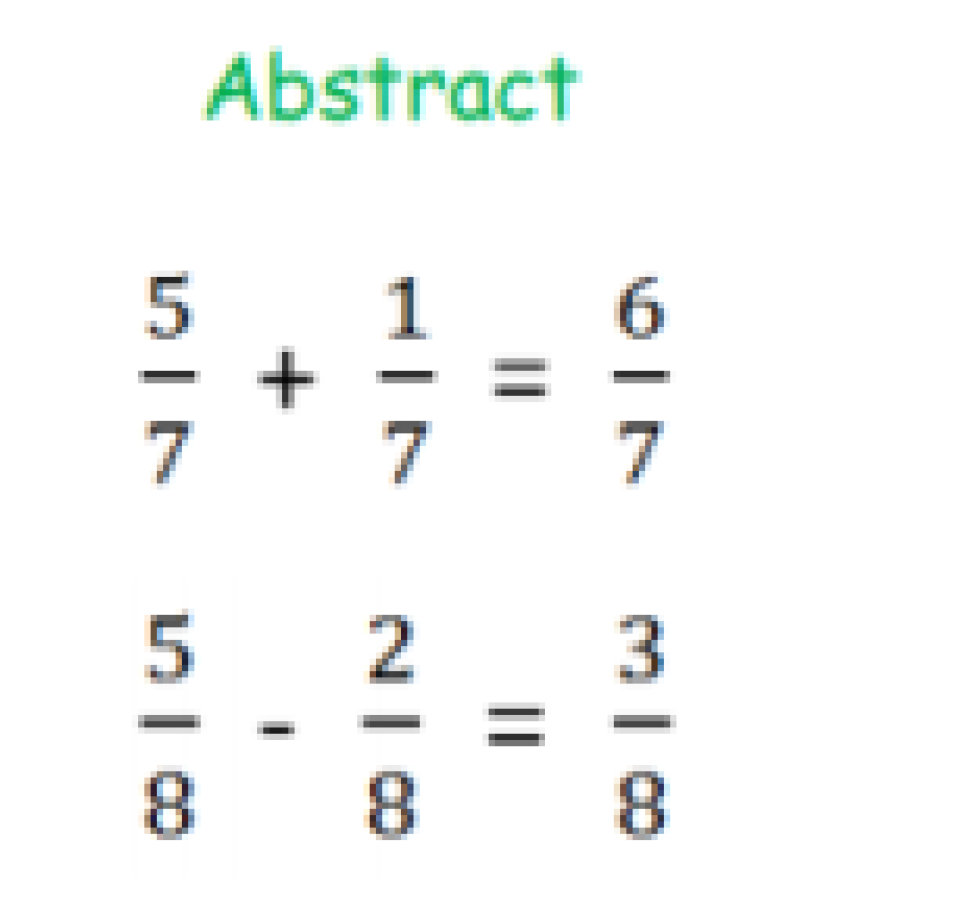
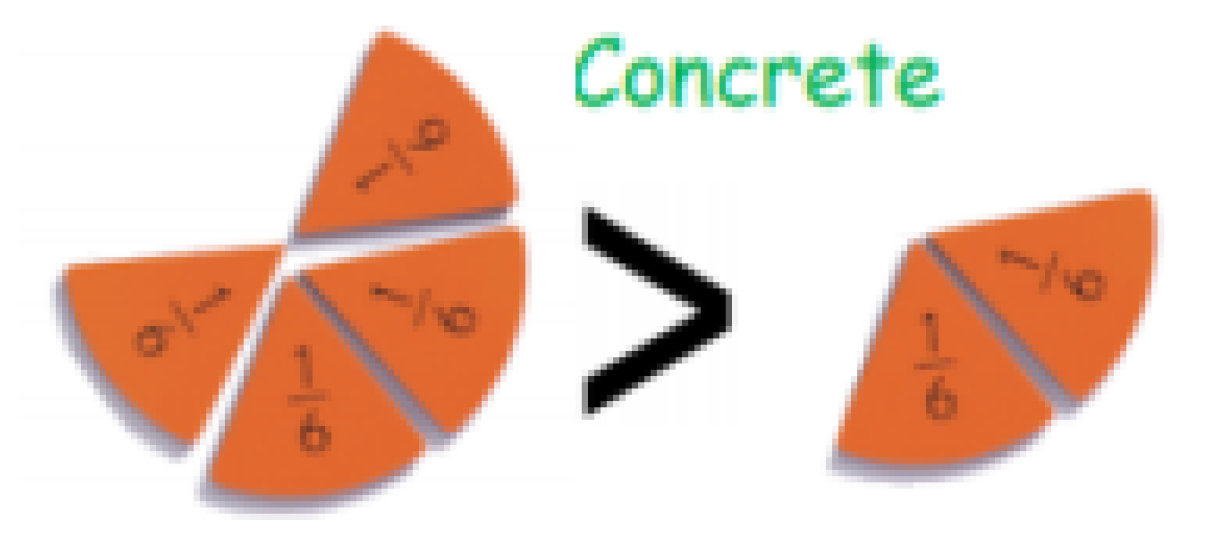
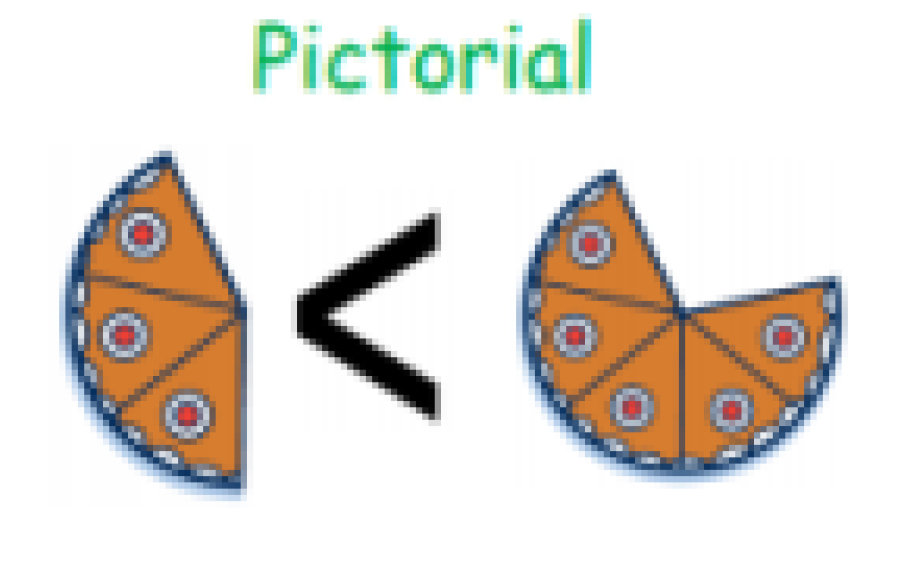
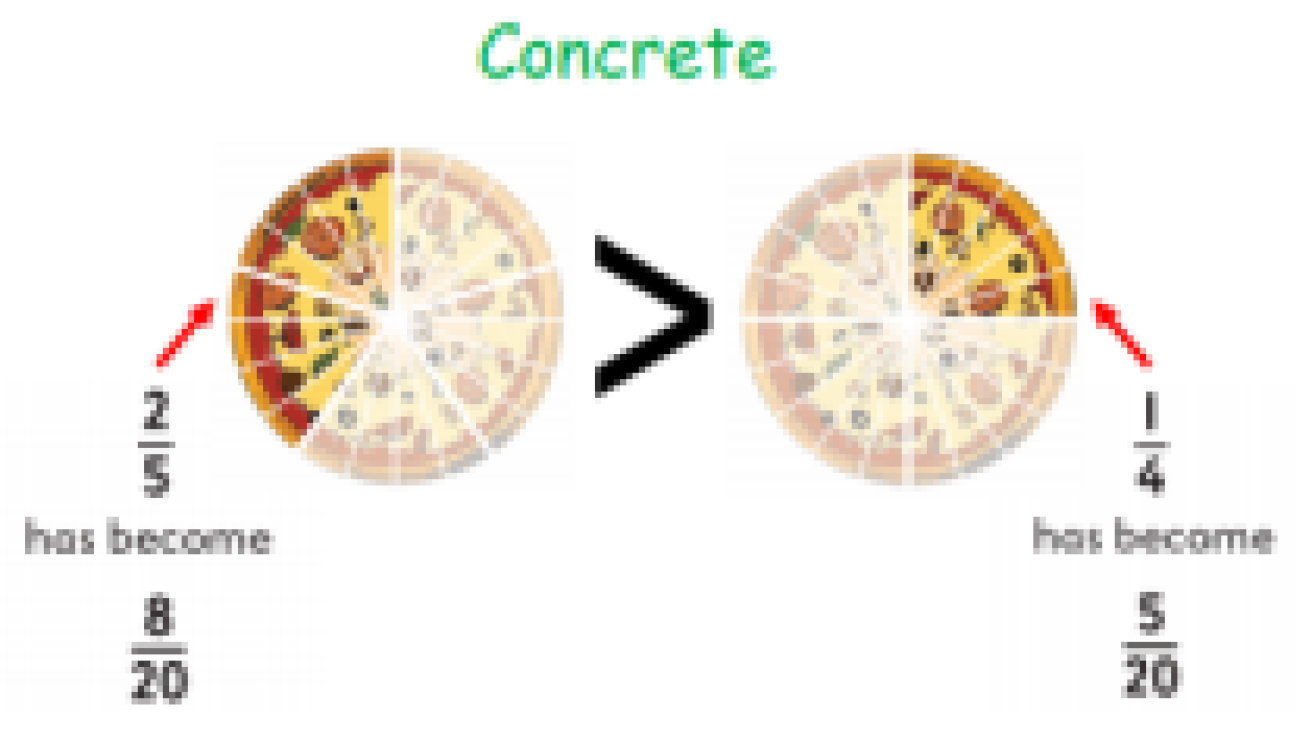
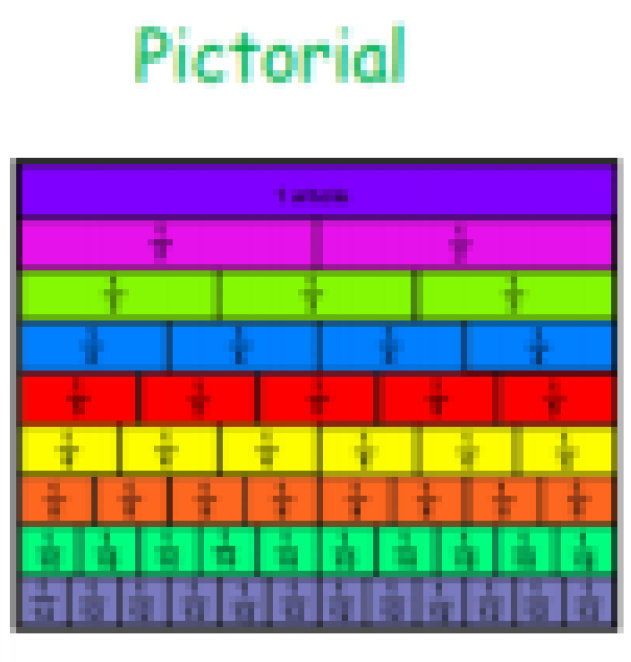
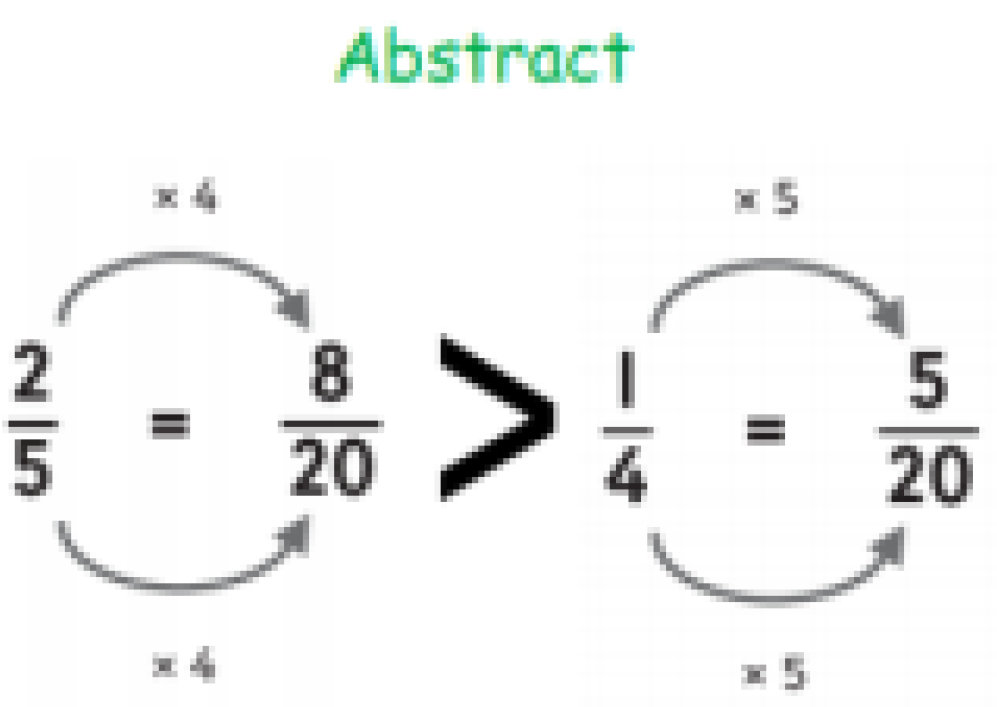
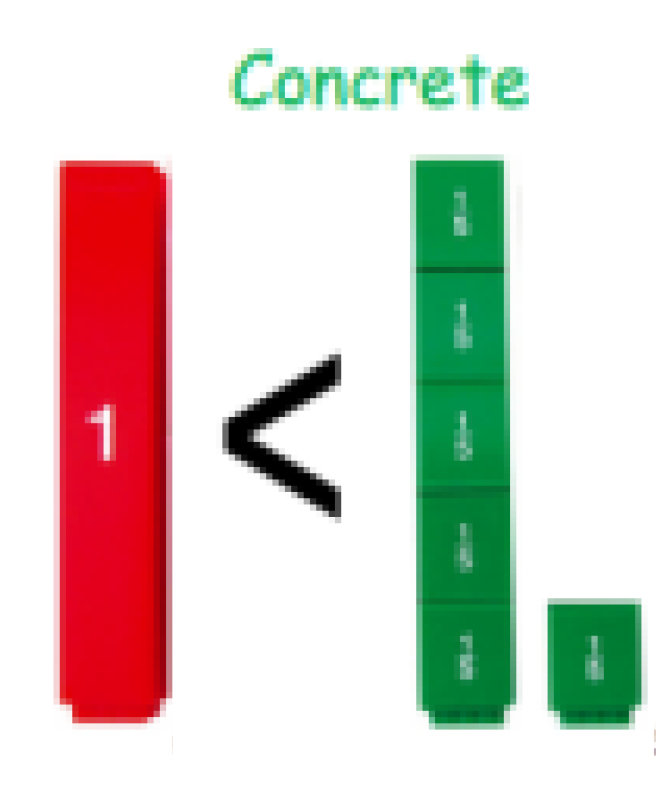
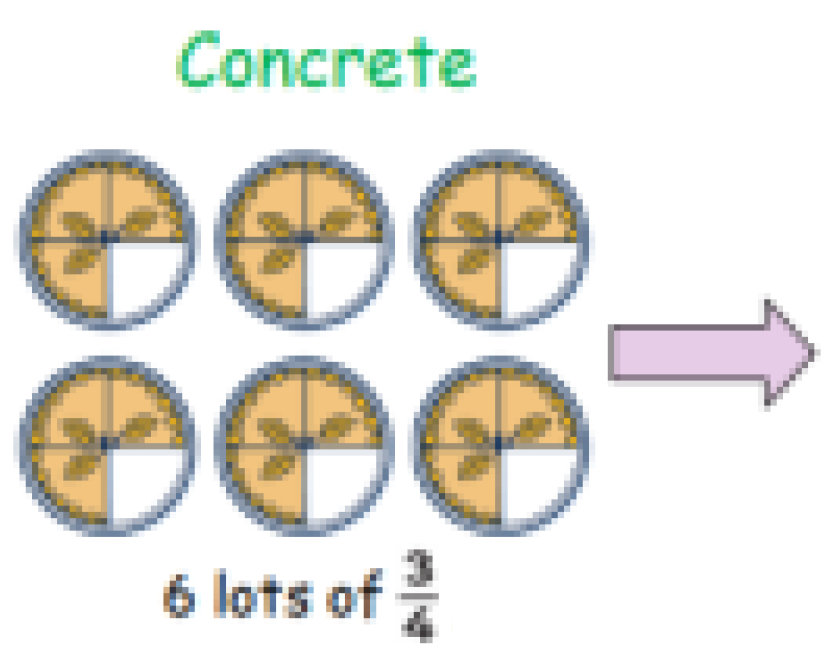
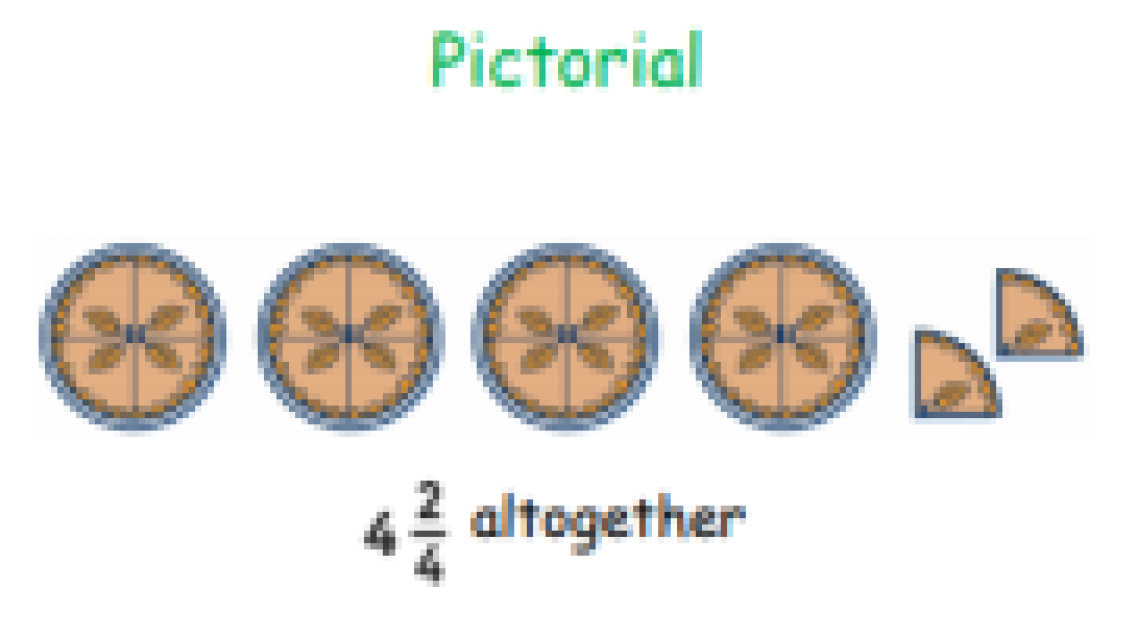
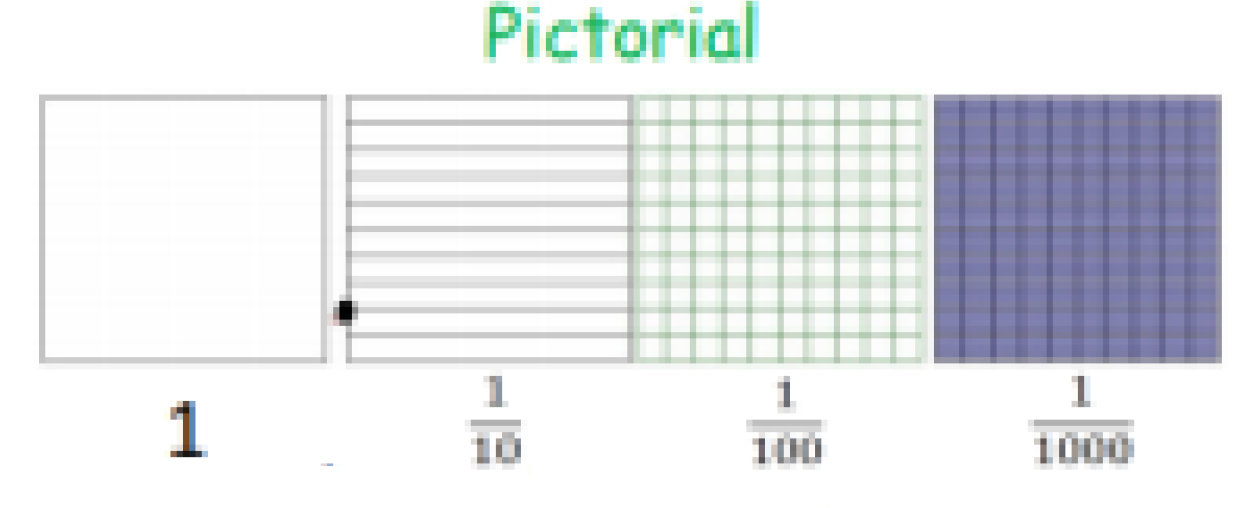
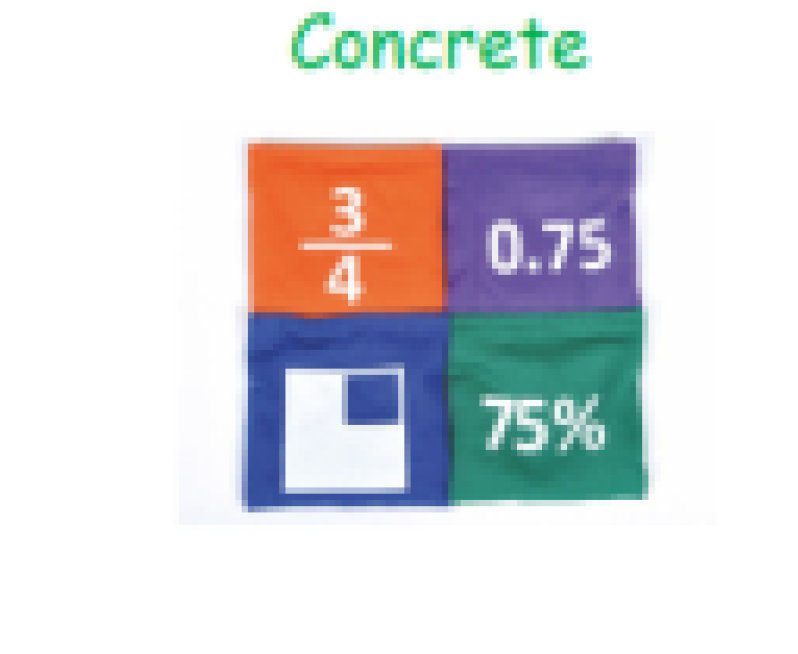
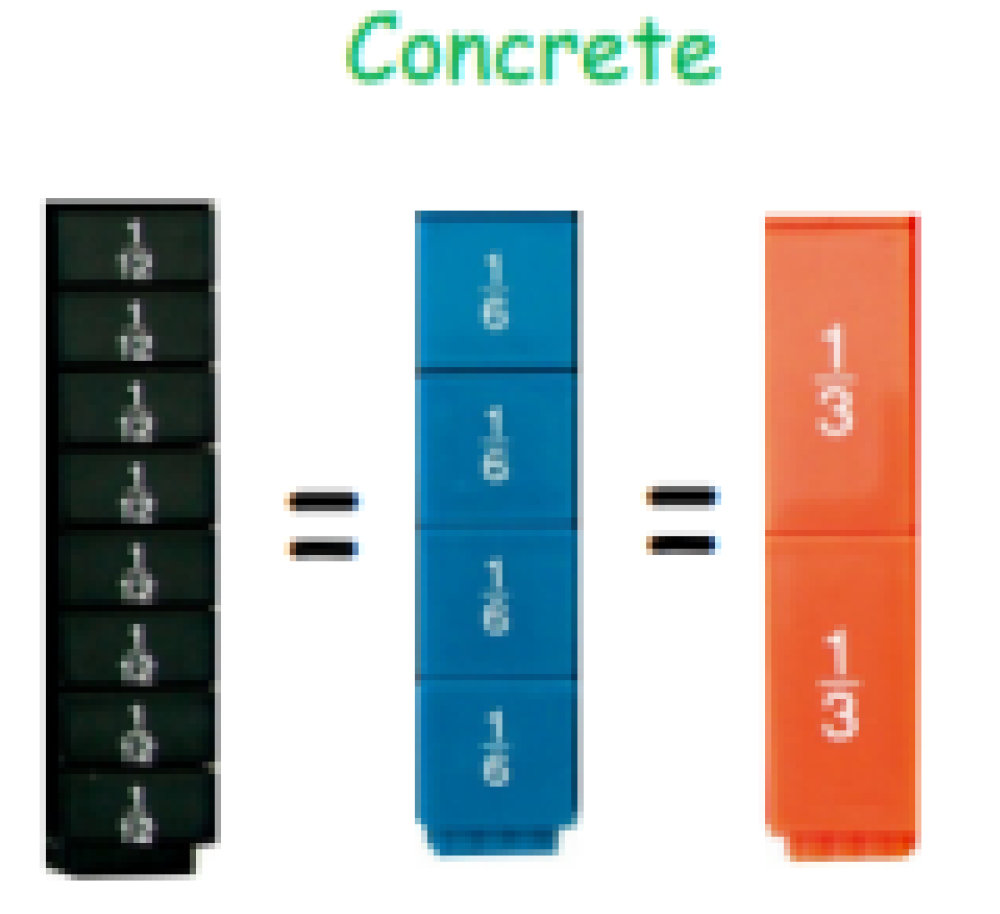
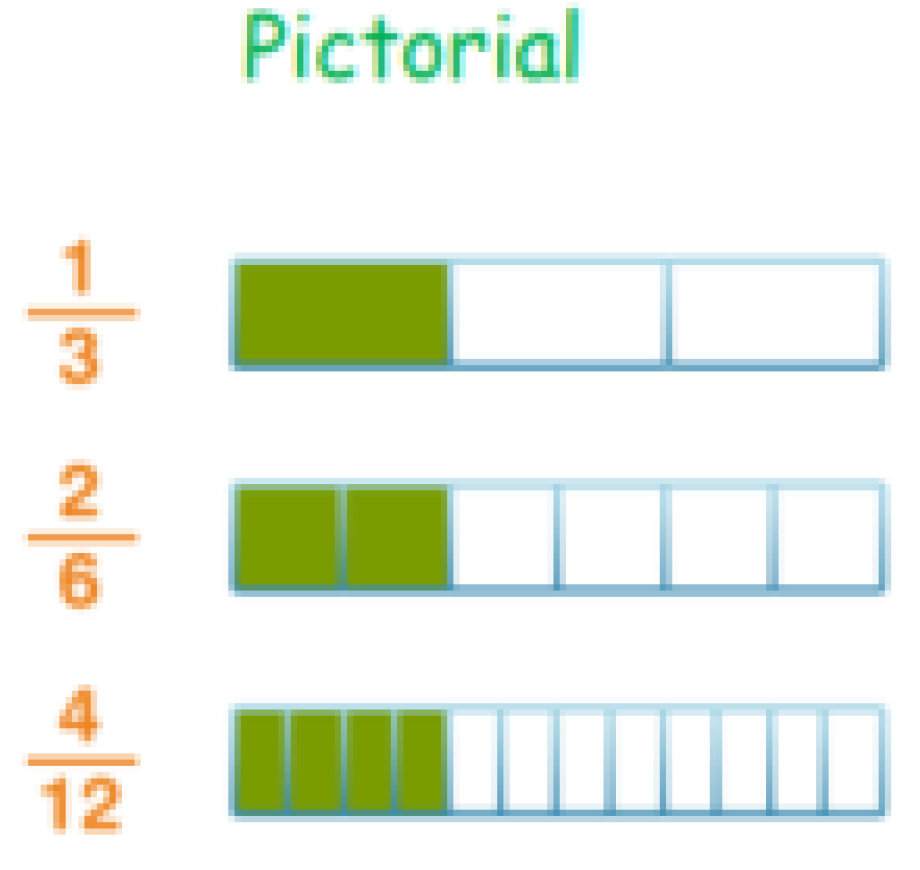
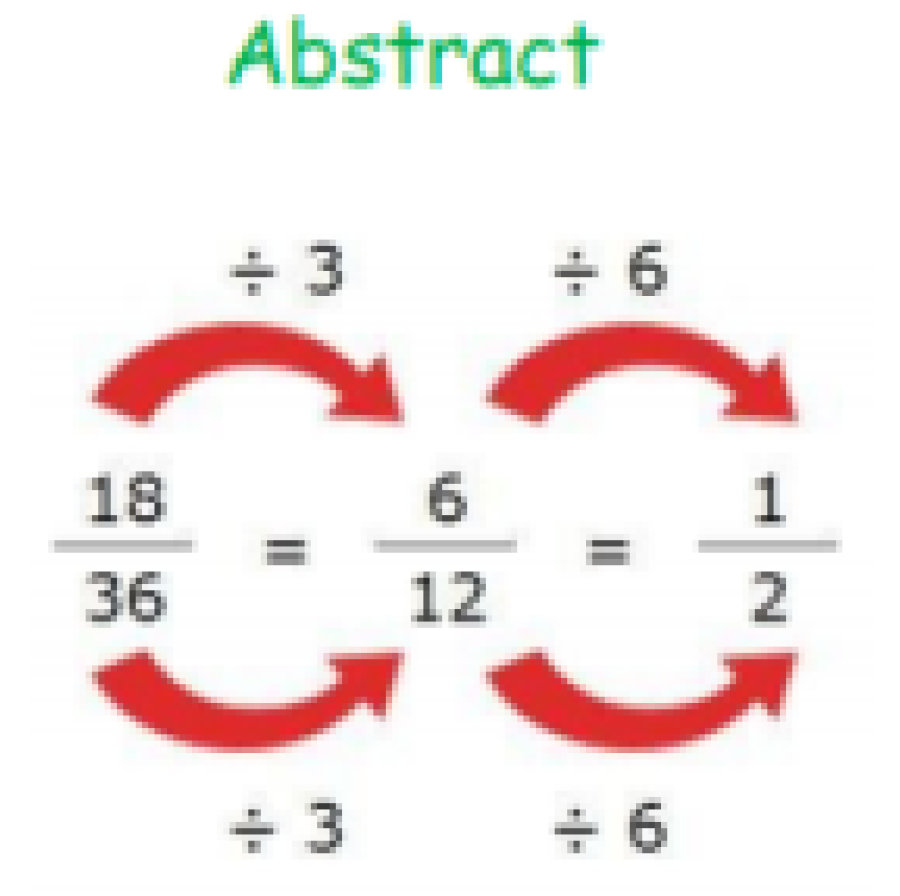
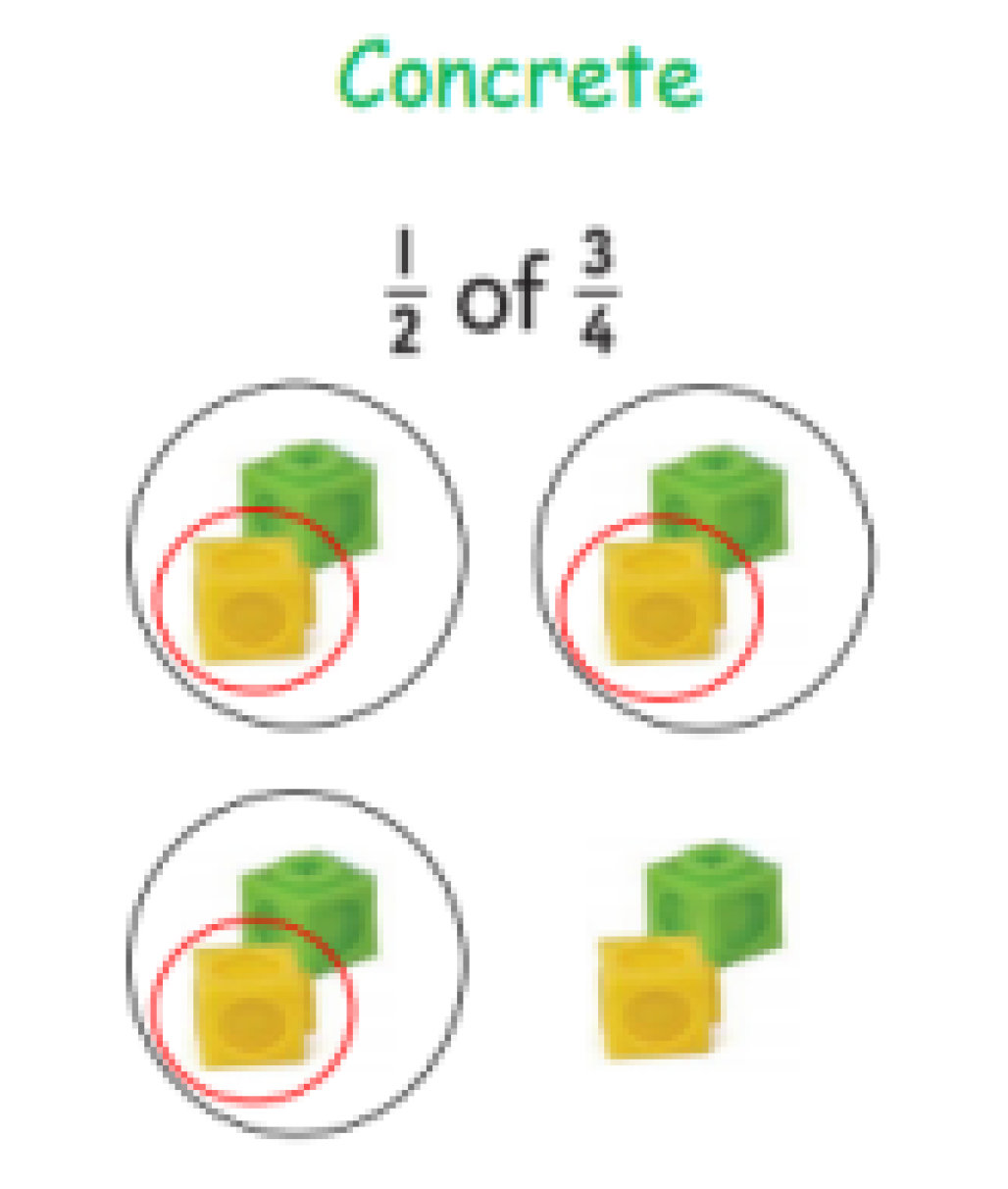
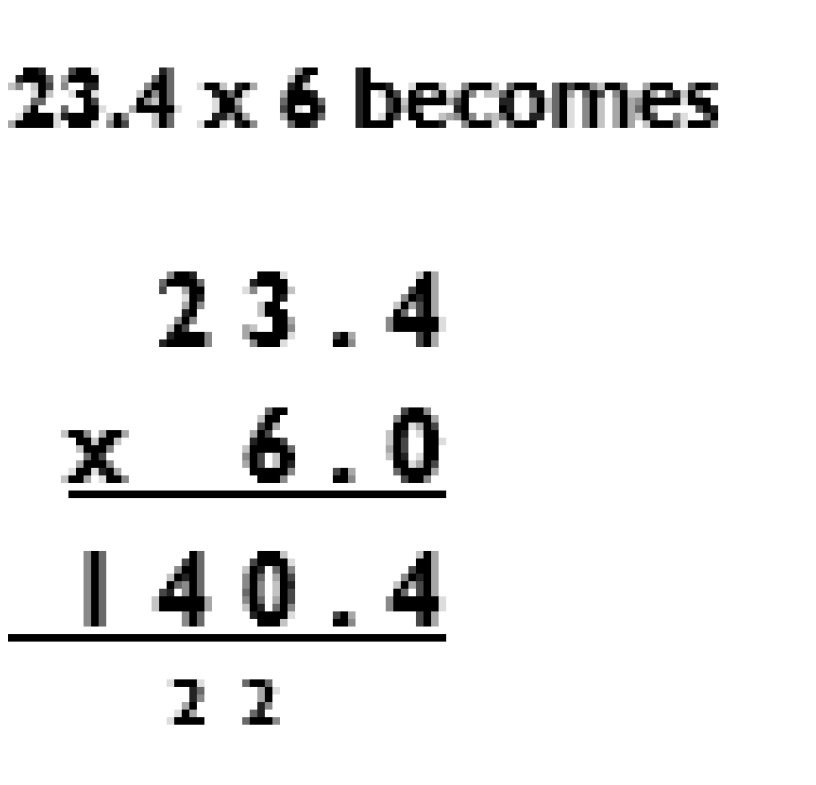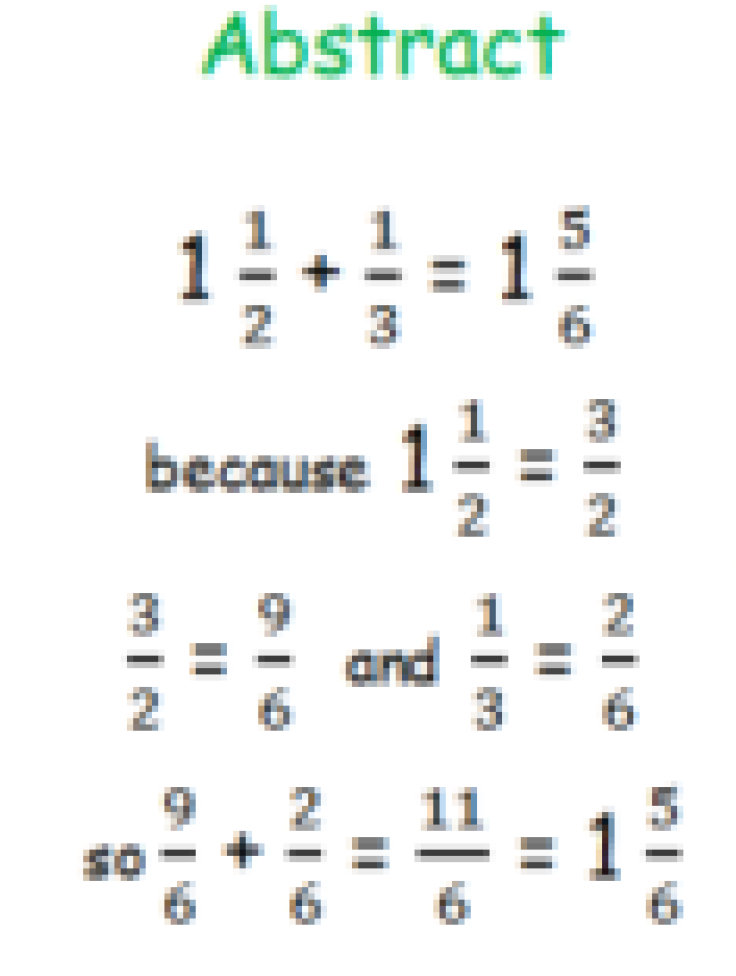Calculation Policy for Mathematics
Ingleton Primary School
Calculation Policy for
Mathematics
Reviewed September 2022
Ingleton Primary School – Calculations Policy
This policy is based on the National Curriculum 2014 and helps to develop the three main aims of Fluency, Reasoning and Problem Solving. It is designed to give pupils a consistent and smooth progression of learning when using the four main operations.
The calculations policy is organised according to age expectations as set out in the New National Curriculum 2014, however, it is vital that pupils are taught according to the stage they are currently working at.
Please note that early teaching and learning in Reception follows the ‘EYFS’ document.
Aim
- To form a core set of methods that every child will use and build upon.
- To ensure greater consistency in the teaching of written calculations & fraction calculations within school.
- To strengthen continuity and progression of children’s understanding of calculations.
- To build upon and ensure continued use of models and images, visual, concrete and abstract, to develop children’s conceptual understanding.
- To be a guide on the teaching of calculation skills for teachers, teaching assistants and parents.
- Mental and written calculation methods should be taught alongside each other throughout the entirety of this progression. When teaching children to calculate emphasis should be placed on choosing and using the method that is most efficient.
- If a child can complete a calculation mentally or with jottings, they should not be expected to complete a written algorithm.
- Whilst no longer part of the statutory curriculum, children should also be taught when and how to use a calculator appropriately.
Important points to note:
- This booklet is a progression in calculations and any of these methods can and should be utilised in other year groups to support or extend pupils as their personal learning requires.
- It is school policy that when ‘carrying’, the carried numbers should be shown under the bottom equals line (with the exception of long multiplication in which carried numbers will be shown above the calculation).
- Pupils should use the ‘one digit, one square’ mantra when using written methods and when calculating with decimals, the decimal point should not have its own square as it has no inherent place value; it should instead straddle the line between the units/ones column and the tenths column.
Addition
In developing a written method for addition, it is important that children understand the concept of addition, in that it is:
Combining two or more groups to give a total or sum
Increasing an amount
They also need to understand and work with certain principles, i.e. that it is:
the inverse of subtraction
commutative i.e. 5 + 3 = 3 + 5
associative i.e. 5 + 3 + 7 = 5 + (3 + 7)
The fact that it is commutative and associative means that calculations can be rearranged, e.g.
4 + 13 = 17 is the same as 13 + 4 = 17.
Contents
Year 1 – Add 1 digit and 2 digit numbers to 20 including 0
Year 2 – Add with 2-digit numbers
Year 3 – Add numbers with up to 3-digits
Year 4 – Add numbers with up to 4-digits
Year 5 – Add numbers with more than 4 digits, more than 2 numbers.
Year R Early Learning Goal:
Using quantities and objects, children add two single-digit numbers and count on to find the answer.
Children are encouraged to develop a mental picture of the number system in their heads to use for calculation. They should experience practical calculation opportunities using a wide variety of practical equipment, including small world play, role play, counters, cubes etc.
Counting all method
Children will begin to develop their ability to add by using practical equipment to count out the correct amount for each number in the calculation and then combine them to find the total. For example, when calculating 4 + 2, they are encouraged to count out four counters and count out two counters.

To find how many altogether, touch and drag them into a line one at a time whilst counting.
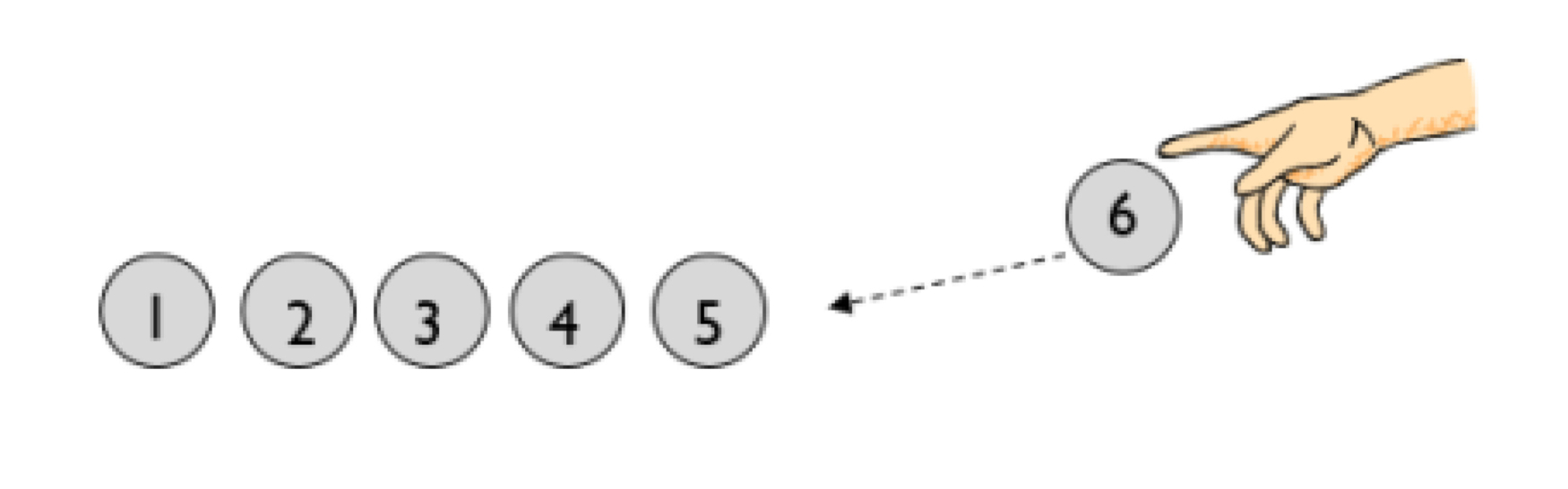
By touch counting and dragging in this way, it allows children to keep track of what they have already counted to ensure they don’t count the same item twice.
Counting on method
To support children in moving from a counting all strategy to one involving counting on, children should still have two groups of objects but one should be covered so that it cannot be counted. For example, when calculating 4 + 2, count out the two groups of counters as before.

then cover up the larger group with a cloth.

For most children, it is beneficial to place the digit card on top of the cloth to remind the children of the number of the counters underneath. They can then start their count at 4, and touch count 5 and 6 in the same way as before, rather than having to count all of the counters separately as before.
Those who are ready may record their own calculations
Year 1 Add 1 digit and 2 digit numbers to 20 including 0
+ = signs and missing numbers
Children need to understand the concept of equality when using the ‘=’ sign. Calculations should be written either side of the equality sign so that the sign is not just interpreted as ‘the answer’.
2 = 1+ 1
2 + 3 = 4 + 1
Missing numbers need to be placed in all possible places.
3 + 4 = • • = 3 + 4
3 + • = 7 7 = • + 4
Add with numbers up to 20
Use numbered number lines to add, by counting on in ones. Encourage children to start with larger number and count on..
The labelled number line
- Children begin to use numbered lines to support their calculations counting on in ones.

To help children develop a sound understanding of numbers and to be able to use them confidently in calculation, there needs to progression in their use of number tracks and number lines.
In addition to their work with numberlines, children should also become familiarwith the use of ‘Base 10’ practical equipment as this will be utilised later in the progression.
Children will continue to use practical equipment, combining groups of objects to find the total by counting all or counting on. Using their developing understanding of place value, they will move on to be able to use Base 10 equipment to make teens numbers using separate tens and units.
For example, when adding 11 and 5, they can make the 11 using a ten rod and a unit.

The units can then be combined to aid with seeing the final total, e.g.

so 11 + 5 = 16. If possible, they should use two different colours of base 10 equipment so that the initial amounts can still be seen.
Children should:
Have access to a wide range of counting equipment, everyday objects, number tracks and number lines, and be shown numbers in different contexts.
Read and write the addition (+) and equals (=) signs within number sentences.
Interpret addition number sentences and solve missing box problems,
using concrete objects and number line addition to solve them: 8 + 3 =
15 + 4 = 5 + 3 + 1 = + = 6
Key vocabulary: add, more, plus, and, make, altogether, total, equal to, equals, double, most, count on, number line
Key skills for addition at Y1:
Read and write numbers to 100 in numerals, incl. 1—20 in words
Recall bonds to 10 and 20, and addition facts within 20
Count to and across 100
Count in multiples of 1 2, 5 and 10
Solve simple 1-step problems involving addition, using objects, number lines and pictorial representations.
Year 2 Add with 2-digit numbers
Developing mental fluency with addition and place value involving 2-digit numbers, then establish more formal methods such as those exemplified in the Y3 section
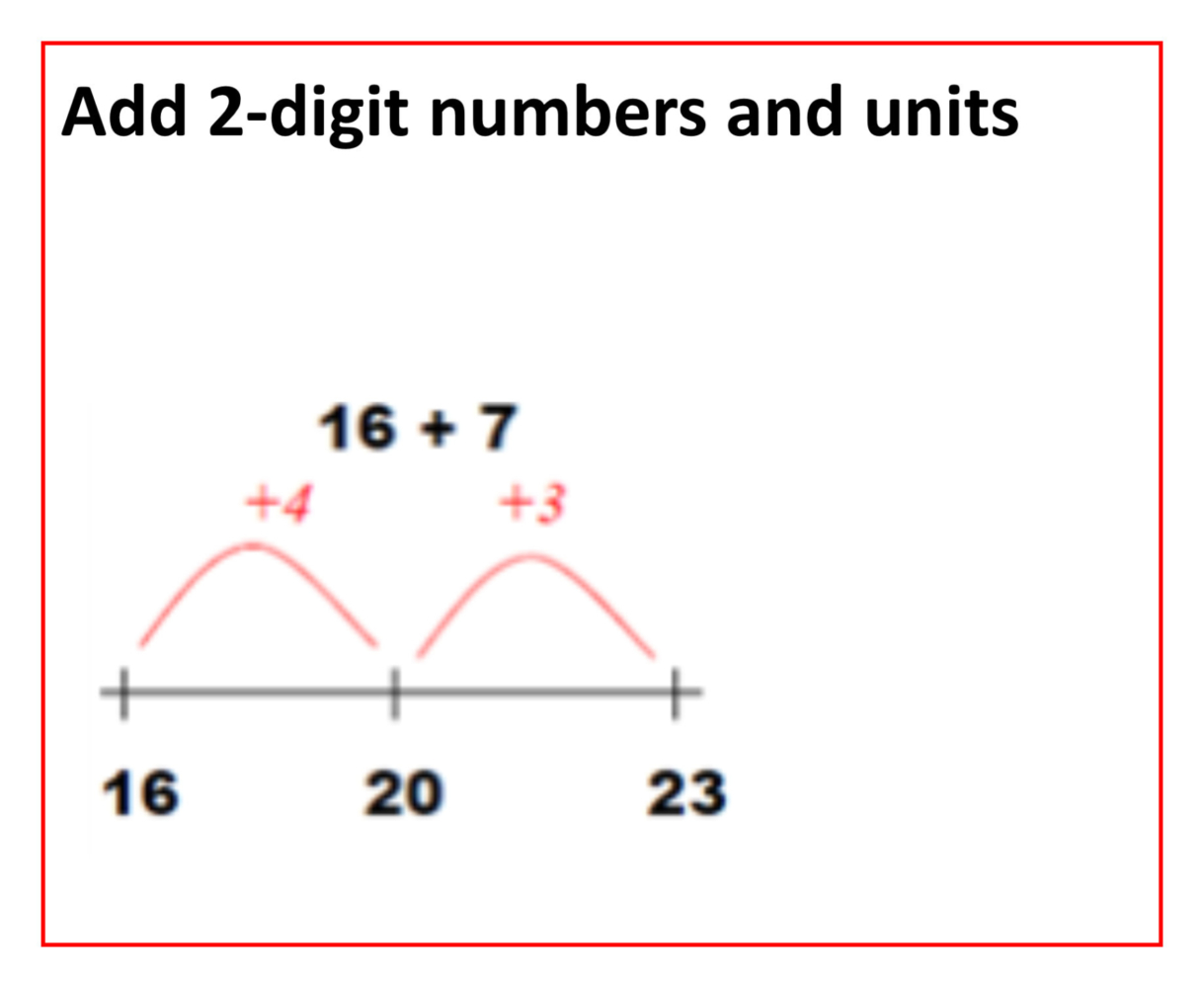

The empty number line is a representation of a mental strategy
Use empty number lines, concrete equipment, hundred squares etc. to build confidence and fluency in mental addition skills.
Add pairs of 2-digit numbers.
First counting on in tens and ones.
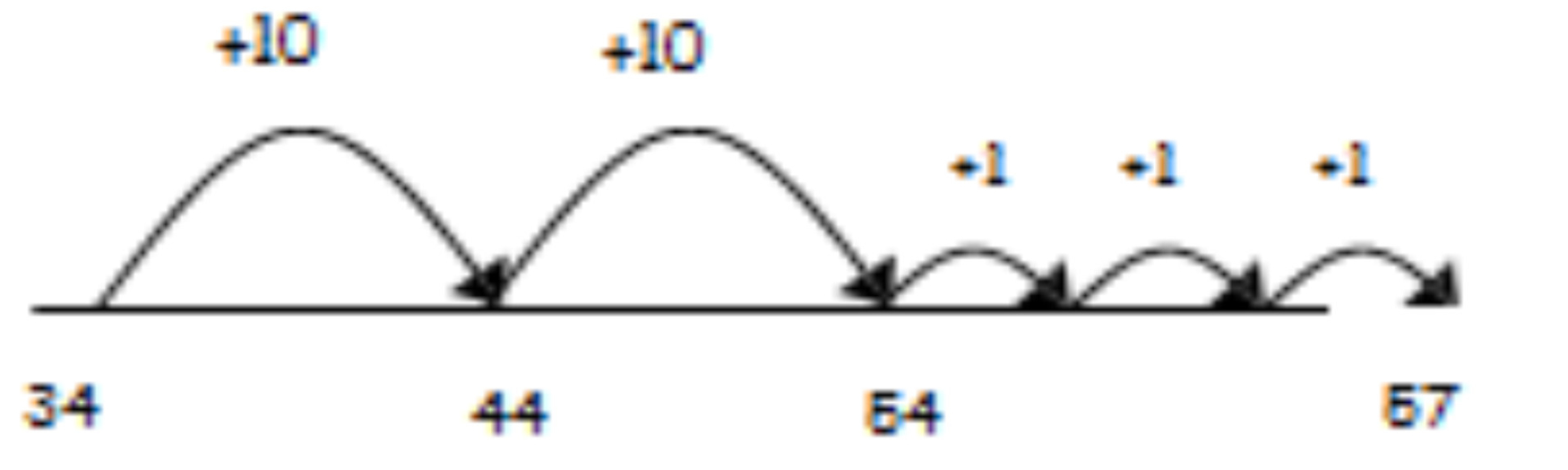
34 + 23 = 57
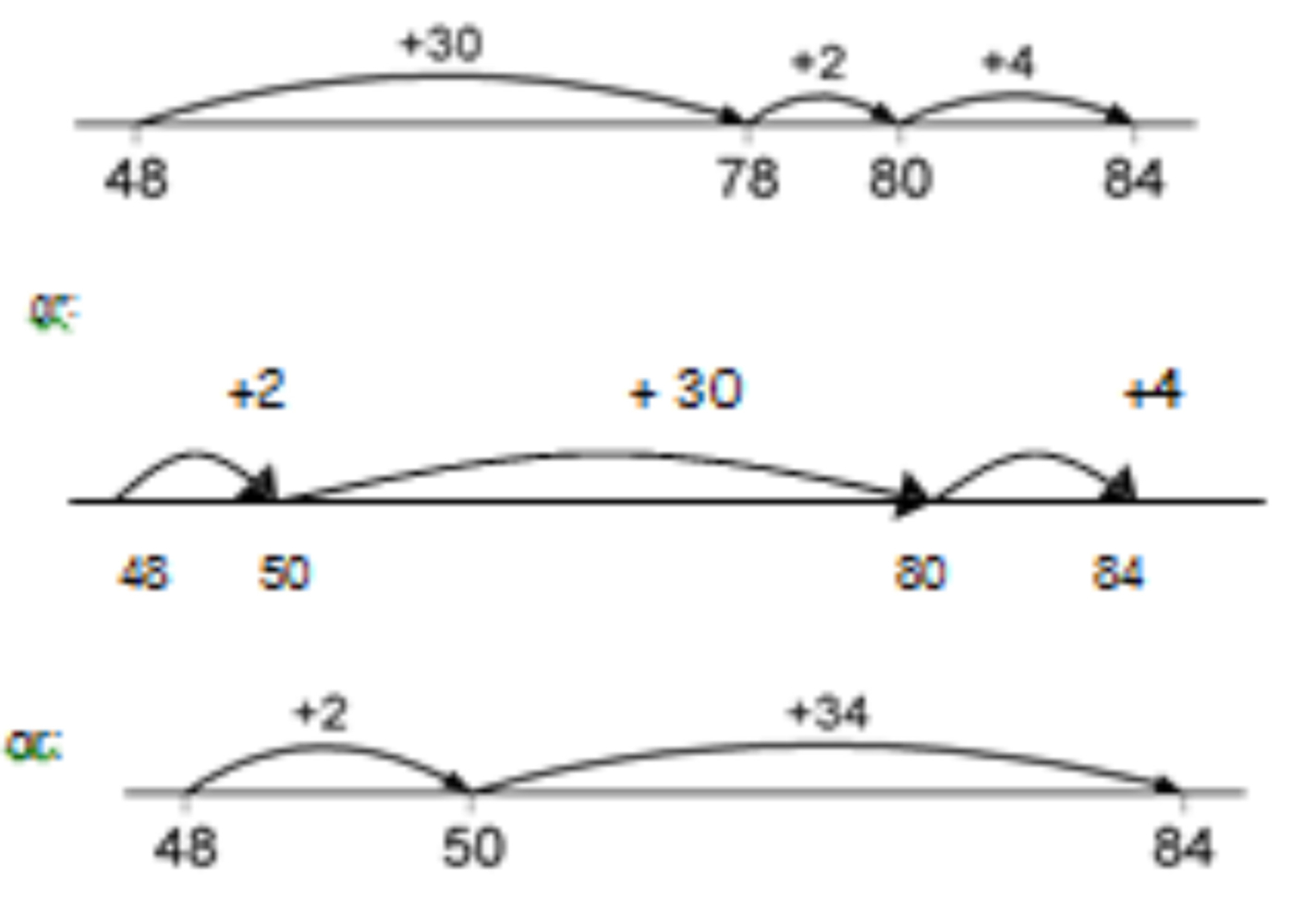
48 + 36
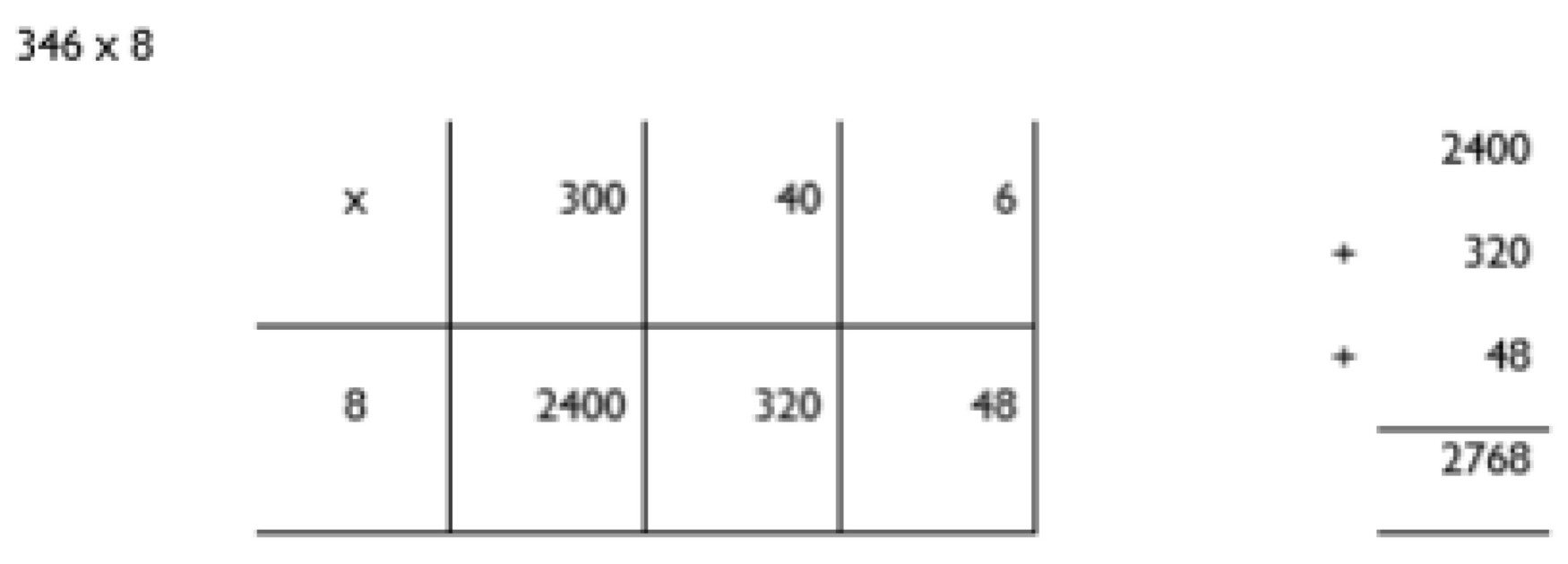
Solve addition problems using the column method involving 2 digit numbers.
Partitioning into tens and ones to lead to a formal written method
- The next stage is to record mental methods using partitioning into tens and ones separately
Only provide examples that do NOT cross the tens boundary until they are secure with the method itself.
Step 1 Step 2
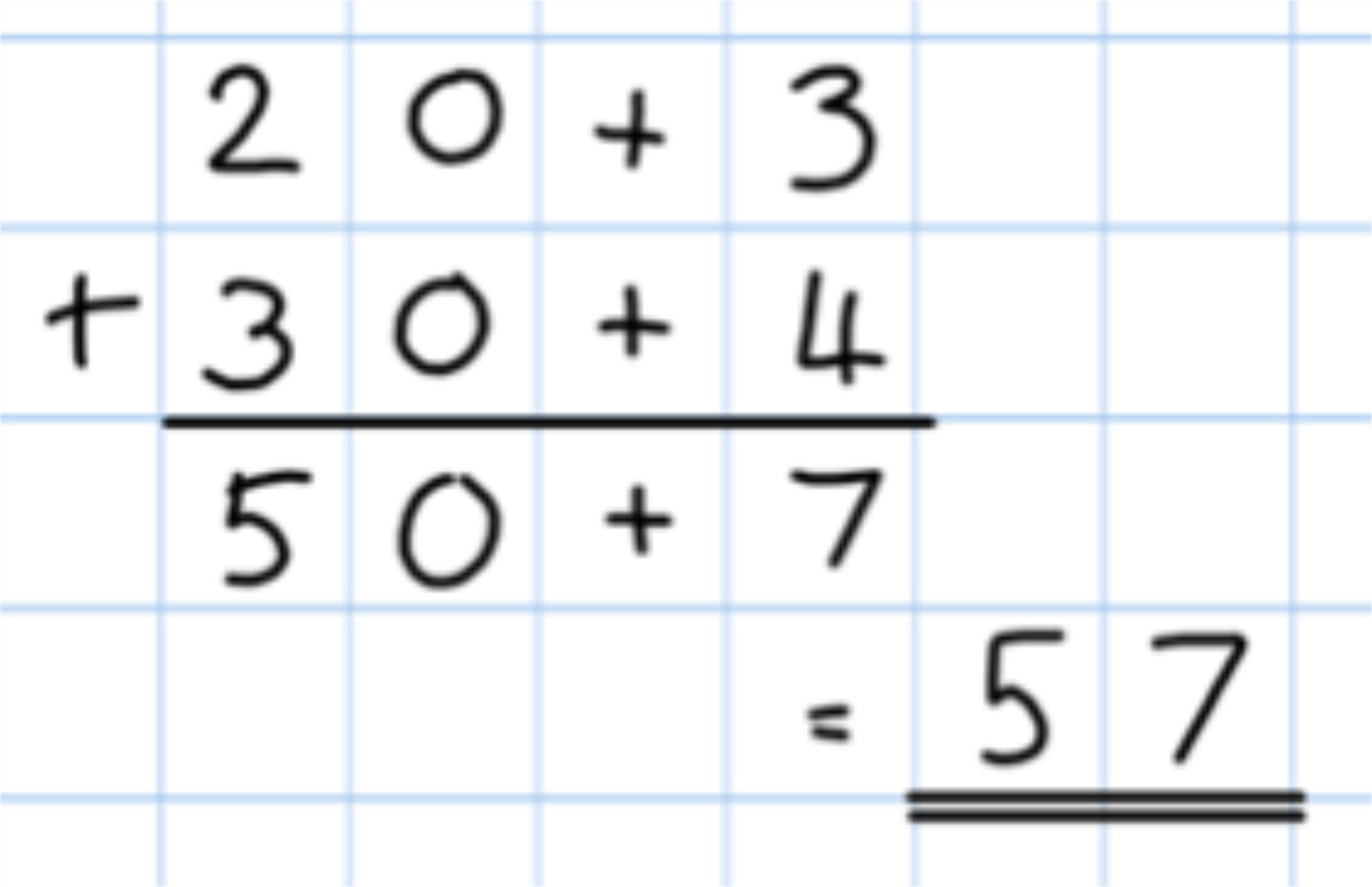

Key vocabulary: add, more, plus, and, make, altogether, total, equal to, equals, double, most, count on, number line, sum, tens, units, partition, addition, column, tens boundary
Key skills for addition at Y2:
Add a 2-digit number and ones (e.g. 27 + 6)
Add a 2-digit number and tens (e.g. 23 + 40)
Add pairs of 2-digit numbers (e.g. 35 + 47) Add three single-digit numbers (e.g. 5 + 9 + 7)
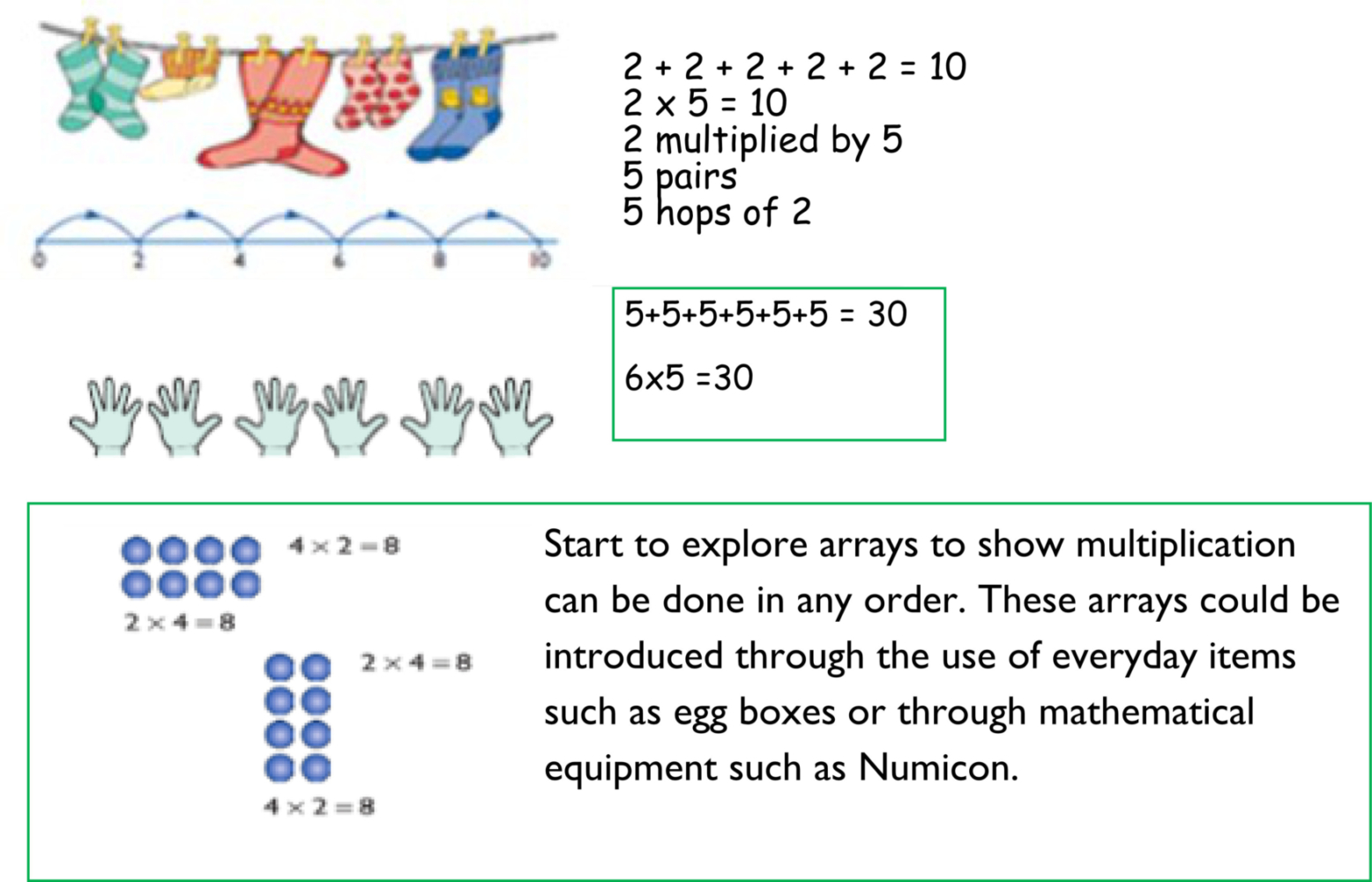
Show that adding can be done in any order (the commutative law).
Recall bonds to 20 and bonds of tens to 100 (30 + 70 etc.)
Count in steps of 2, 3 and 5 and count in tens from any number.
Understand the place value of 2-digit numbers (tens and ones)
Compare and order numbers to 100 using < > and = signs. Read and write numbers to at least 100 in numerals and words.
Solve problems with addition, using concrete objects, pictorial representations, involving numbers, quantities and measures, and applying mental and written methods.
Year 3 Add numbers with up to 3-digits
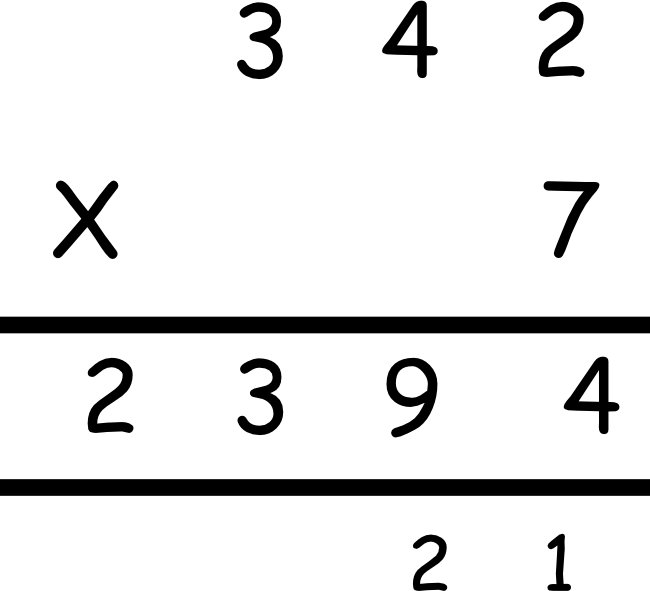
To ensure the statutory final written method is grounded in understanding, this stage connects the practical equipment to the formal written method.
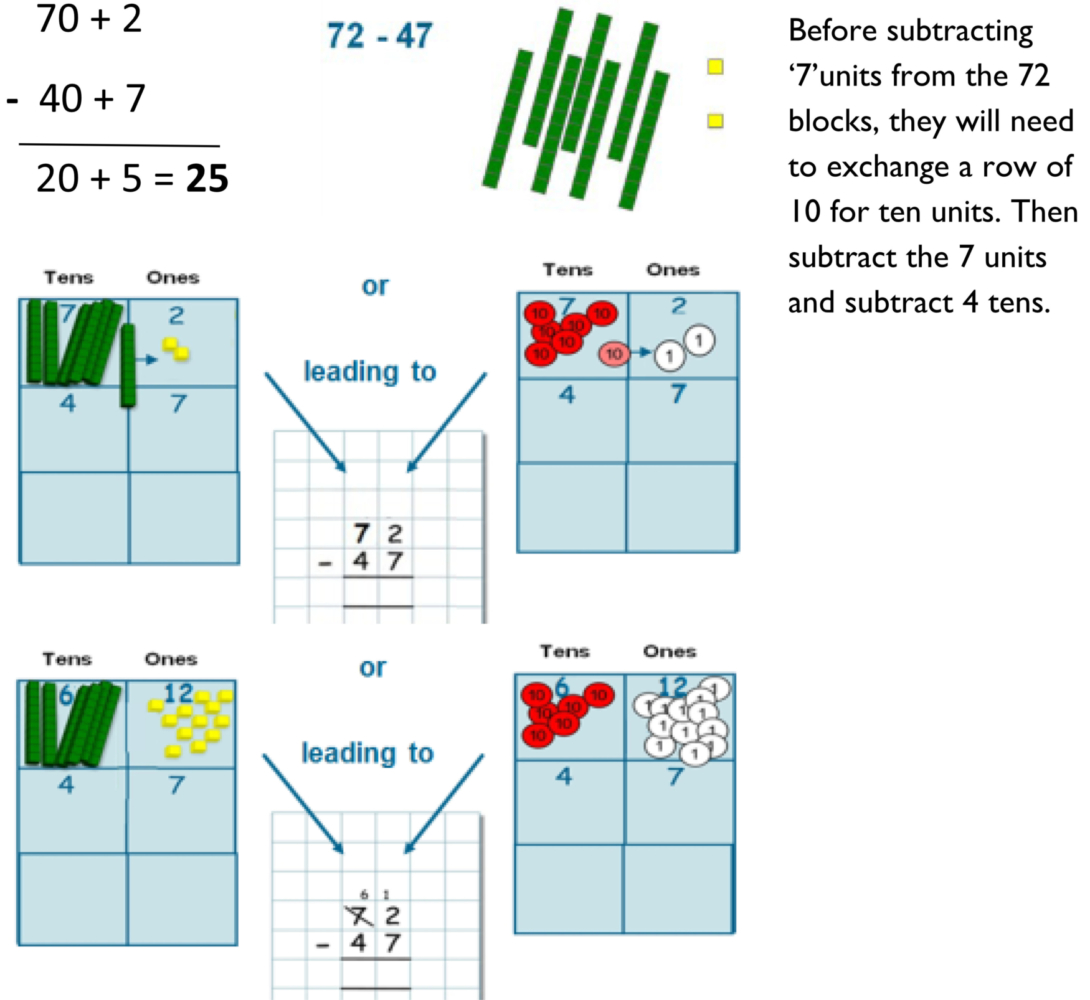
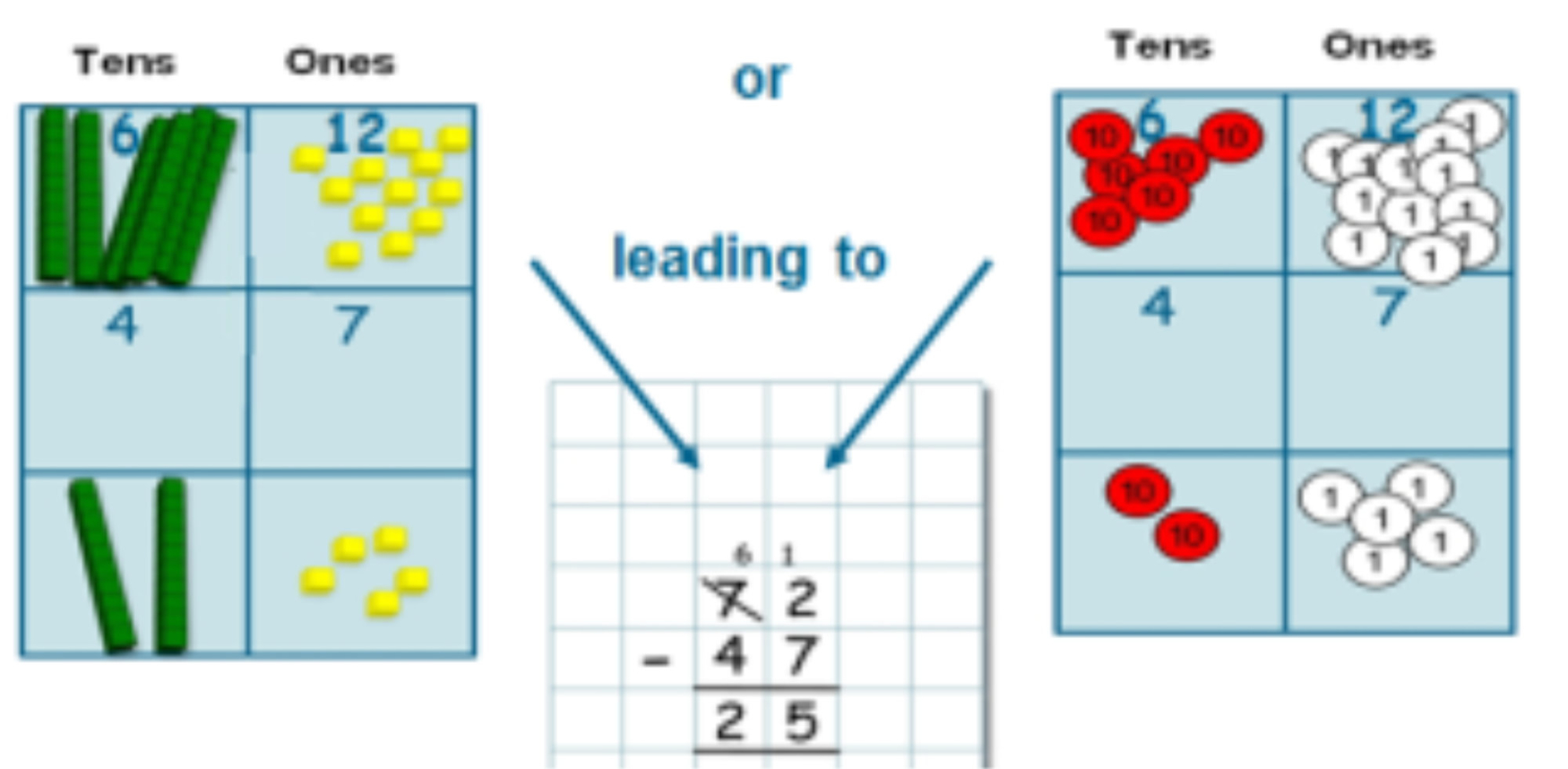
Children first experience the practical version of column addition and when confident in explaining this, including exchanging when crossing the tens barrier with ones, they record the written method alongside.

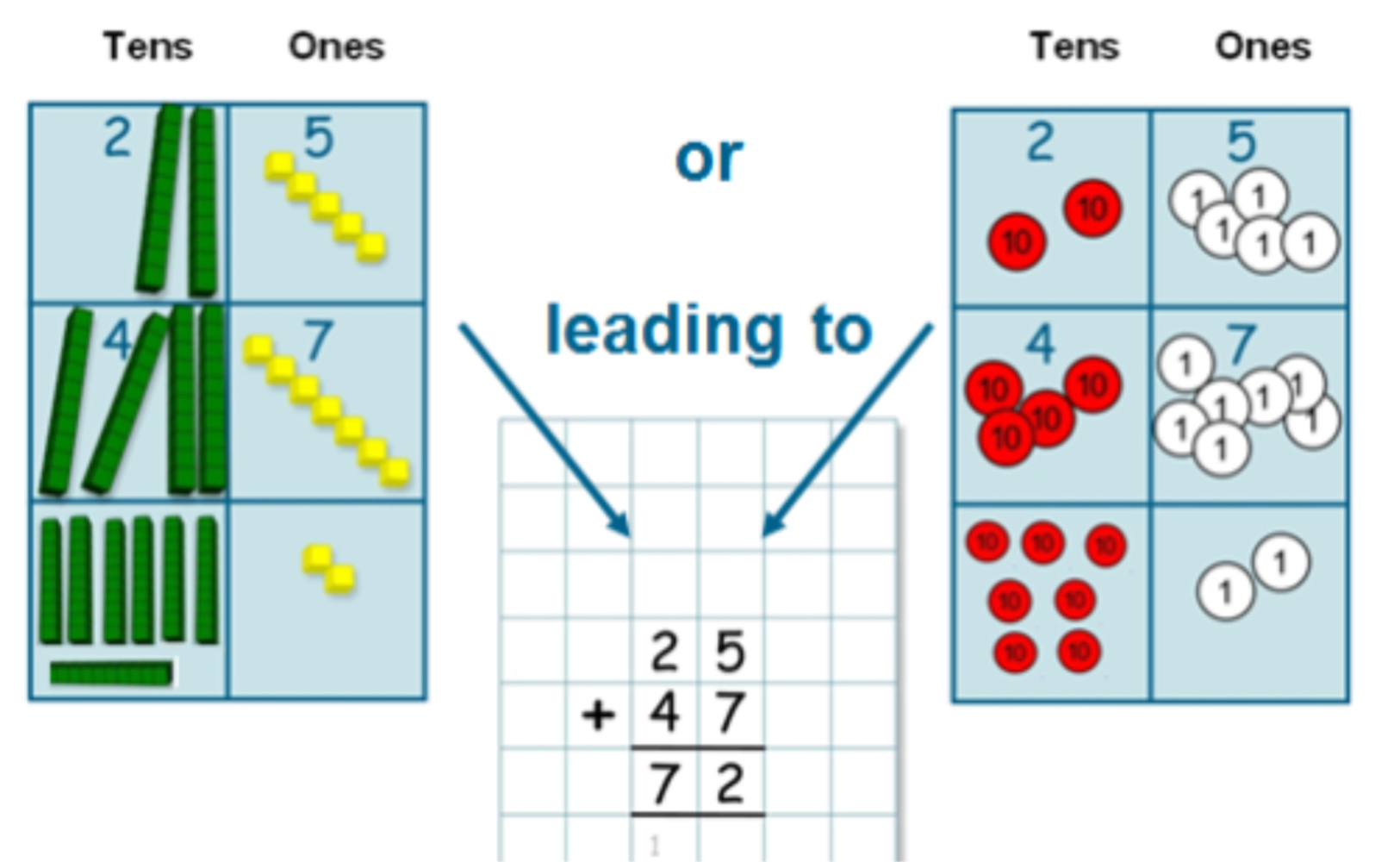
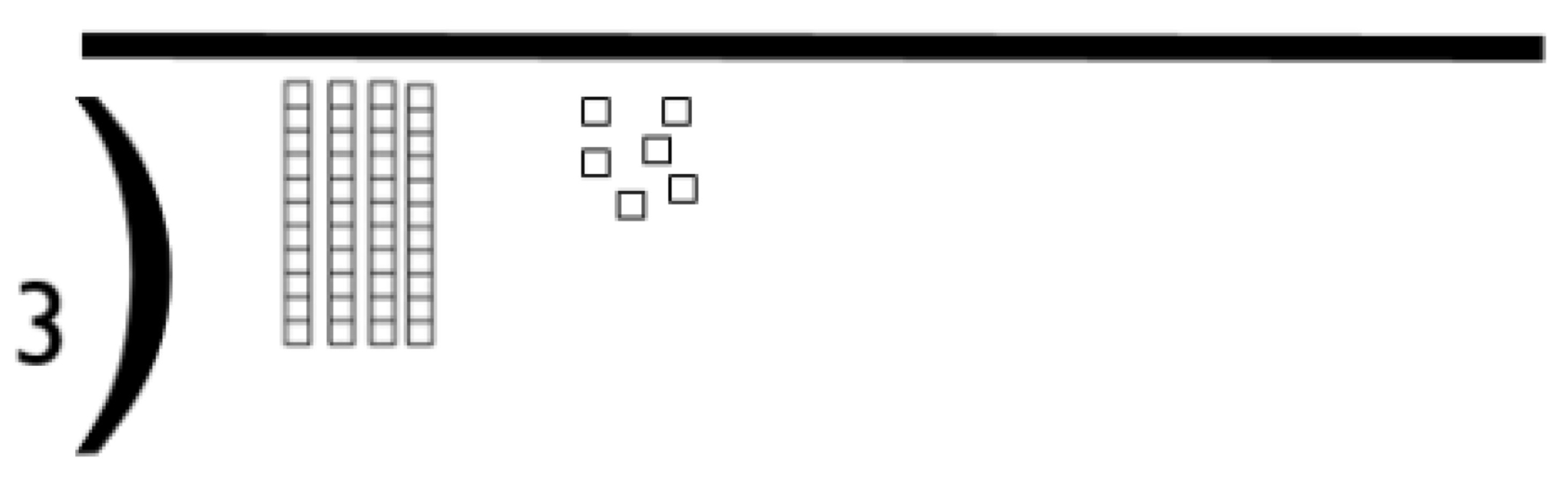
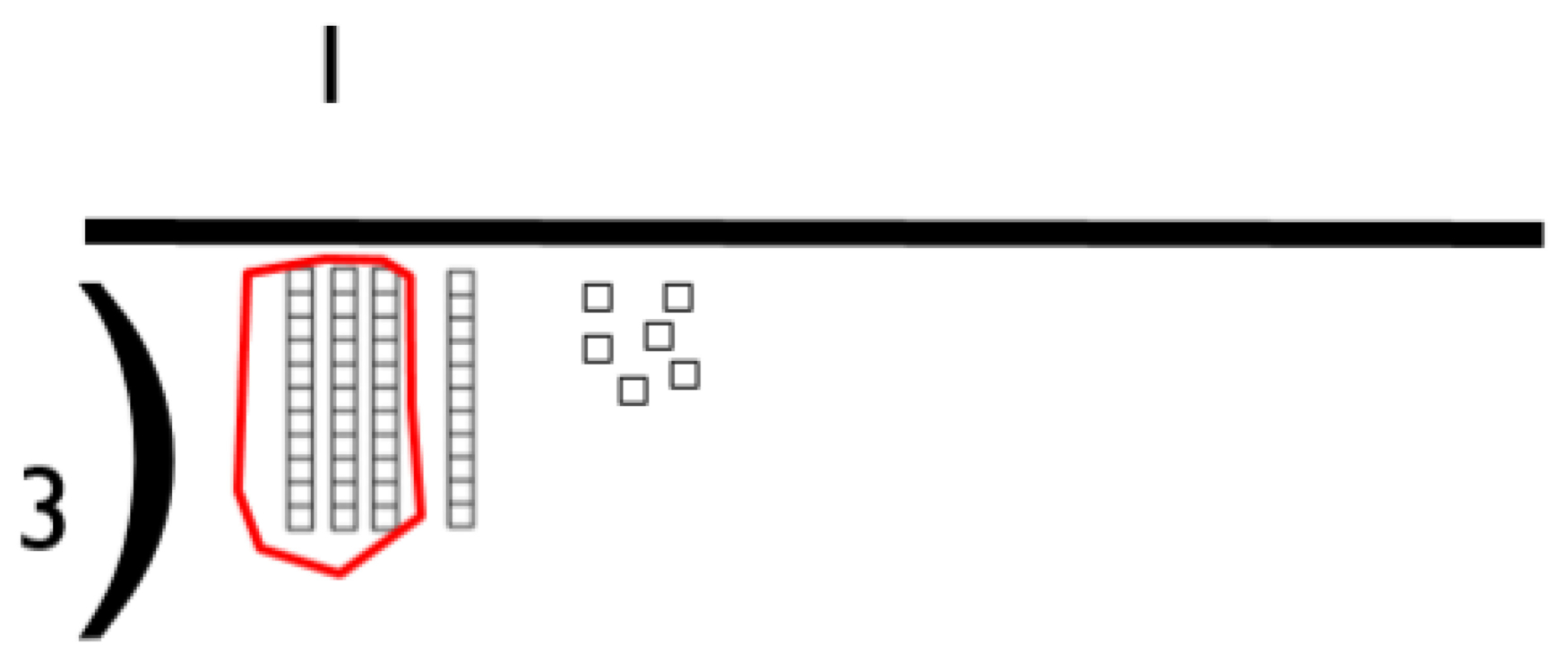
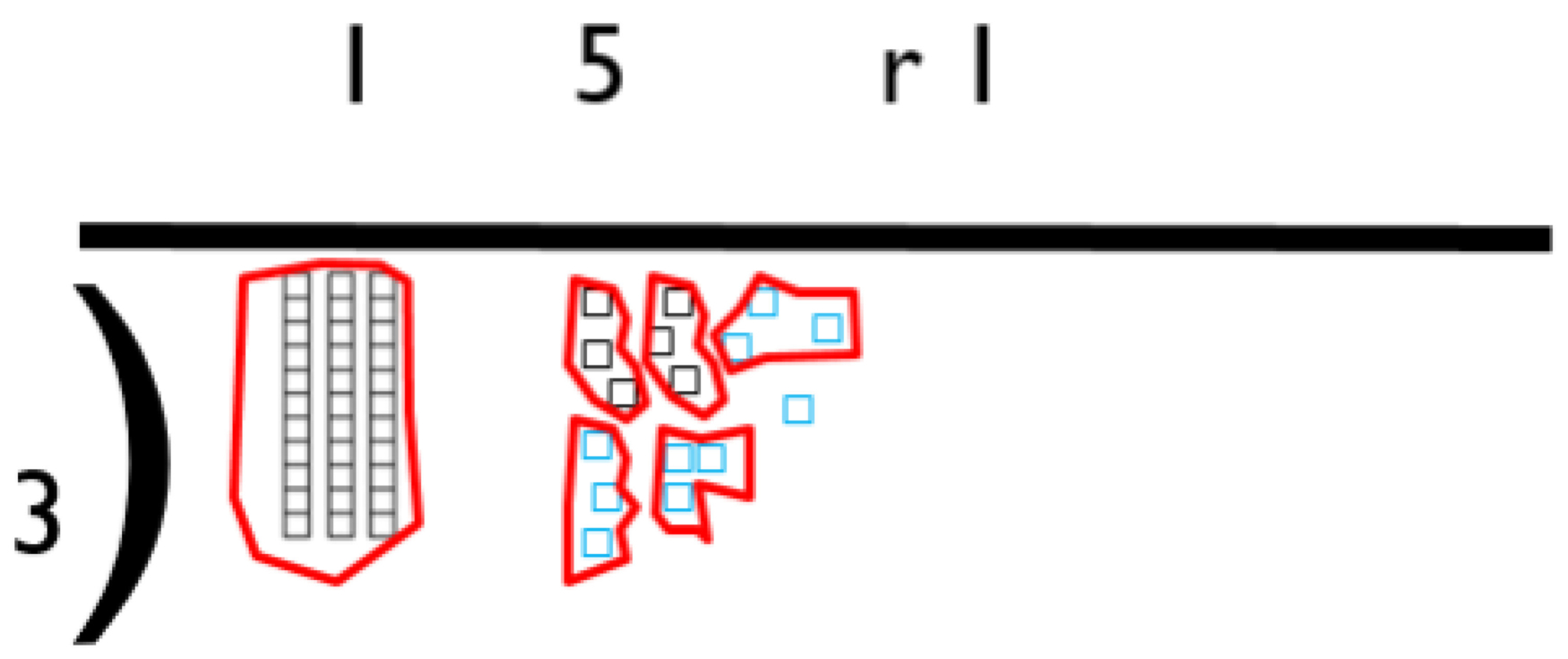
Represented in place value columns and rows. Starting adding with the ‘least significant digit’ . When the tens barriers is crossed in the ‘ones’ exchange then takes place.
Children must have a strong understanding of place value to complete this stage.
Tips:
- Add units/ones first.
- Remember the actual value is “two tens add four tens”, not “two add four”, which equals six tens.
Key vocabulary: add, more, plus, and, make, altogether, total, equal to, equals, double, most, count on, number line, sum, tens, units, partition, plus, addition, column, tens boundary, hundreds boundary, increase, vertical, exchange.
Key skills for addition at Y3:
Read and write numbers to 1000 in numerals and words.
Add 2-digit numbers mentally, incl. those exceeding 100.
Add a three-digit number and ones mentally (175 + 8)
Add a three-digit number and tens mentally (249 + 50)
Add a three-digit number and hundreds mentally (381 + 400)
Estimate answers to calculations, using inverse to check answers.
Solve problems, including missing number problems, using number facts, place value, and more complex addition.
Recognise place value of each digit in 3-digit numbers (hundreds, tens, ones.)
Continue to practise a wide range of mental addition strategies, ie. number bonds, adding the nearest multiple of 10, 100, 100 and adjusting, using near doubles, partitioning and recombining.
Year 4 Add numbers with up to 4-digits
Also include money and measure contexts.
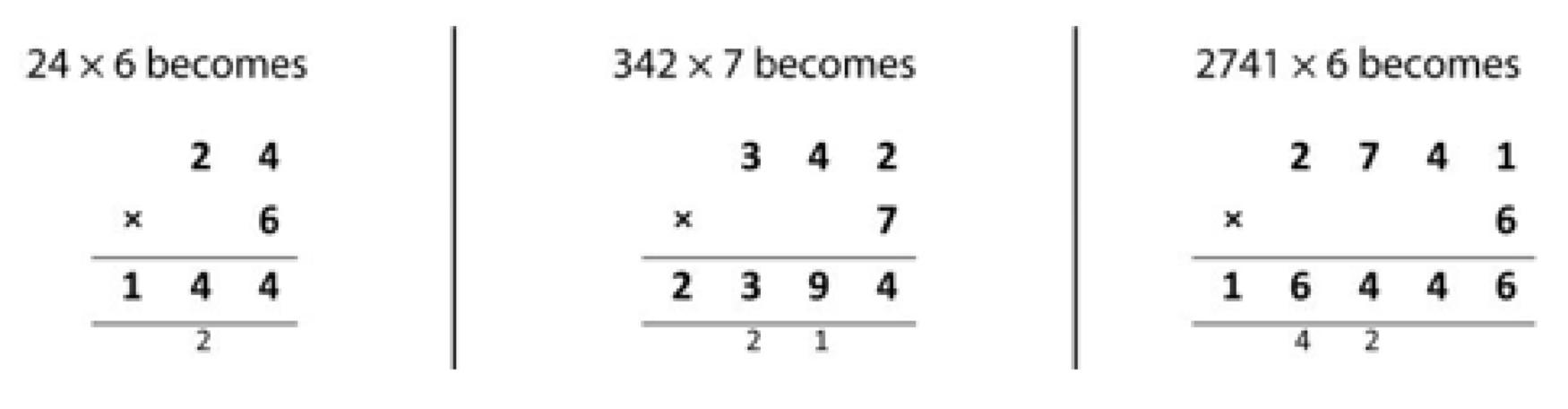
In this method, recording is reduced further. Carried digits are recorded, using the words ‘carry ten’ or ‘carry one hundred’ etc., according to the value of the digit.

Key vocabulary: add, more, plus, and, make, altogether, total, equal to, equals, double, most, count on, number line, sum, tens, units, partition, plus, addition, column, tens boundary, hundreds boundary, increase, vertical, exchange, thousands, hundreds, digits, inverse
Key skills for addition at Y4:
Select most appropriate method: mental, jottings or written and explain why.
Recognise the place value of each digit in a four-digit number.
Round any number to the nearest 10, 100 or 1000.
Estimate and use inverse operations to check answers.
Solve 2-step problems in context, deciding which operations and methods to use and why.
Find 1000 more or less than a given number.
Continue to practise a wide range of mental addition strategies, ie. number bonds, add the nearest multiple of 10, 100, 1000 and adjust, use near doubles, partitioning and recombining.
Add numbers with up to 4 digits using the formal written method of column addition
Solve 2-step problems in contexts, deciding which operations and methods to use and why.
Estimate and use inverse operations to check answers to a calculation.
Year 5 Add numbers with more than 4 digits, more than 2 numbers.
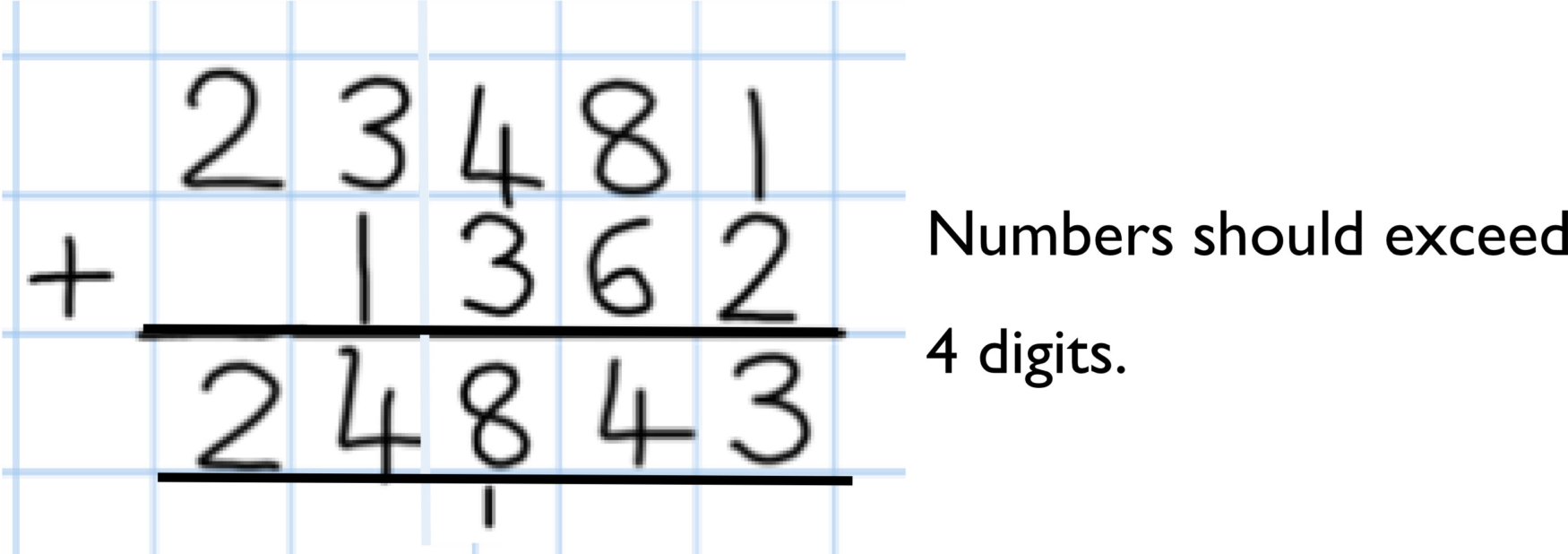


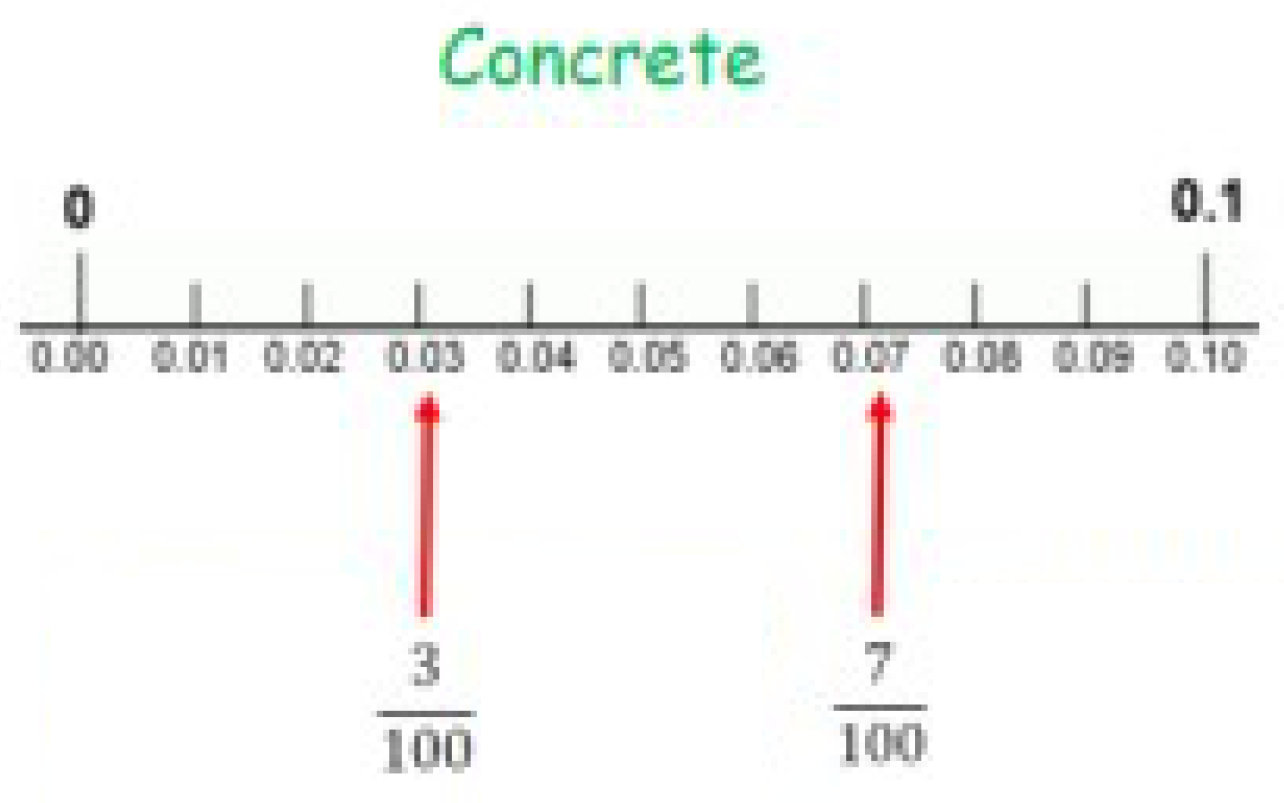
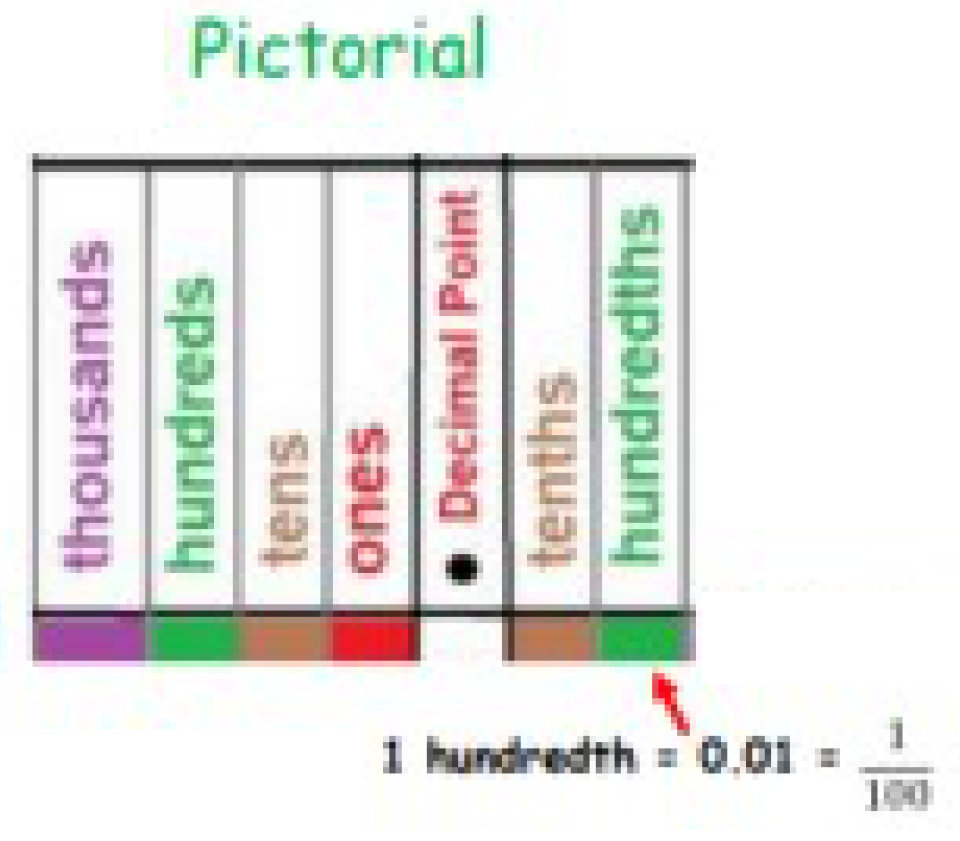
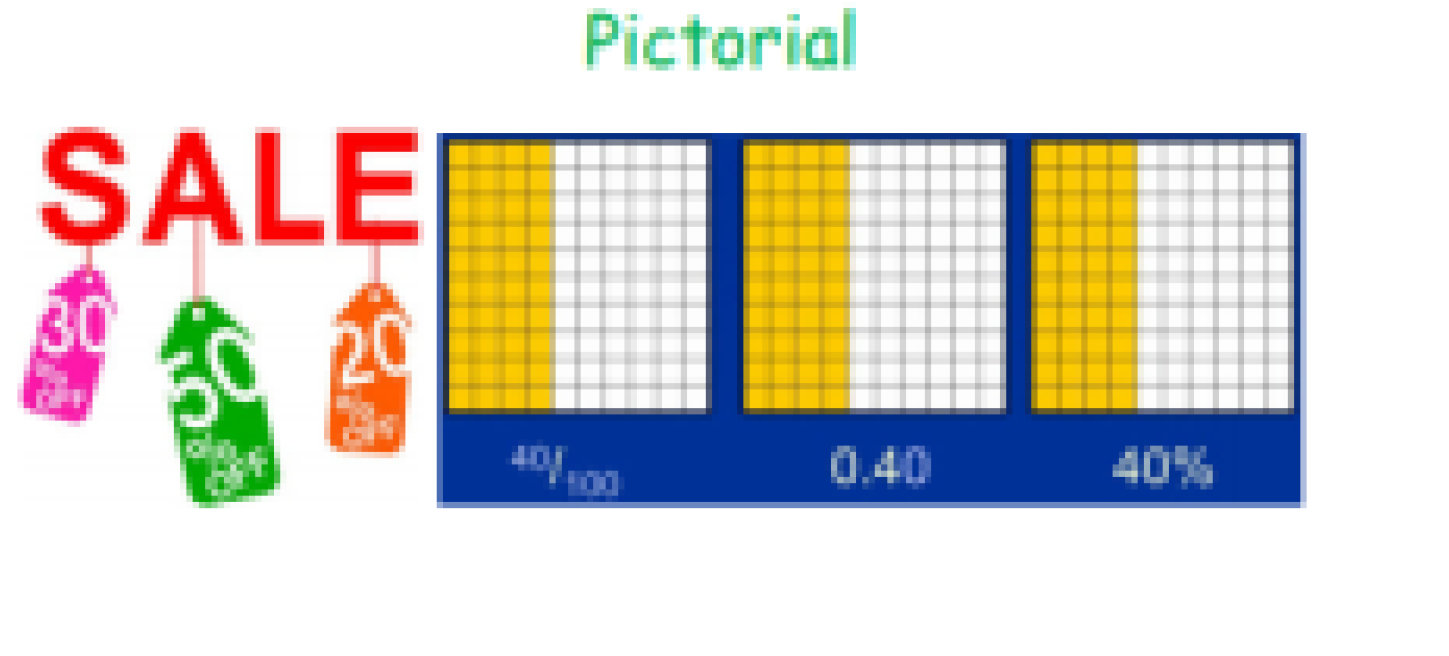
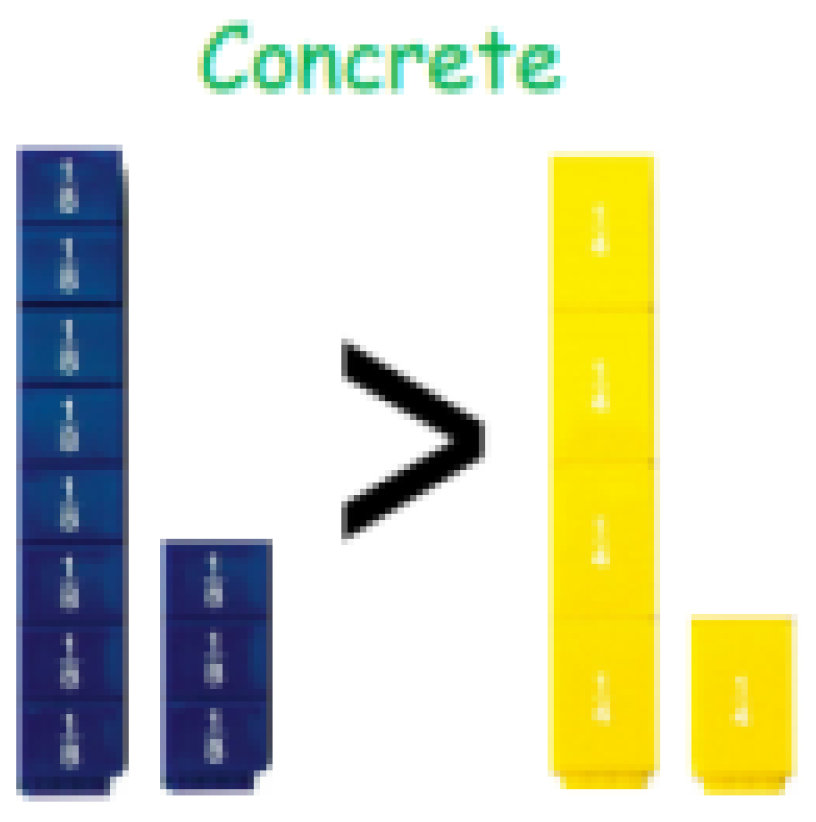
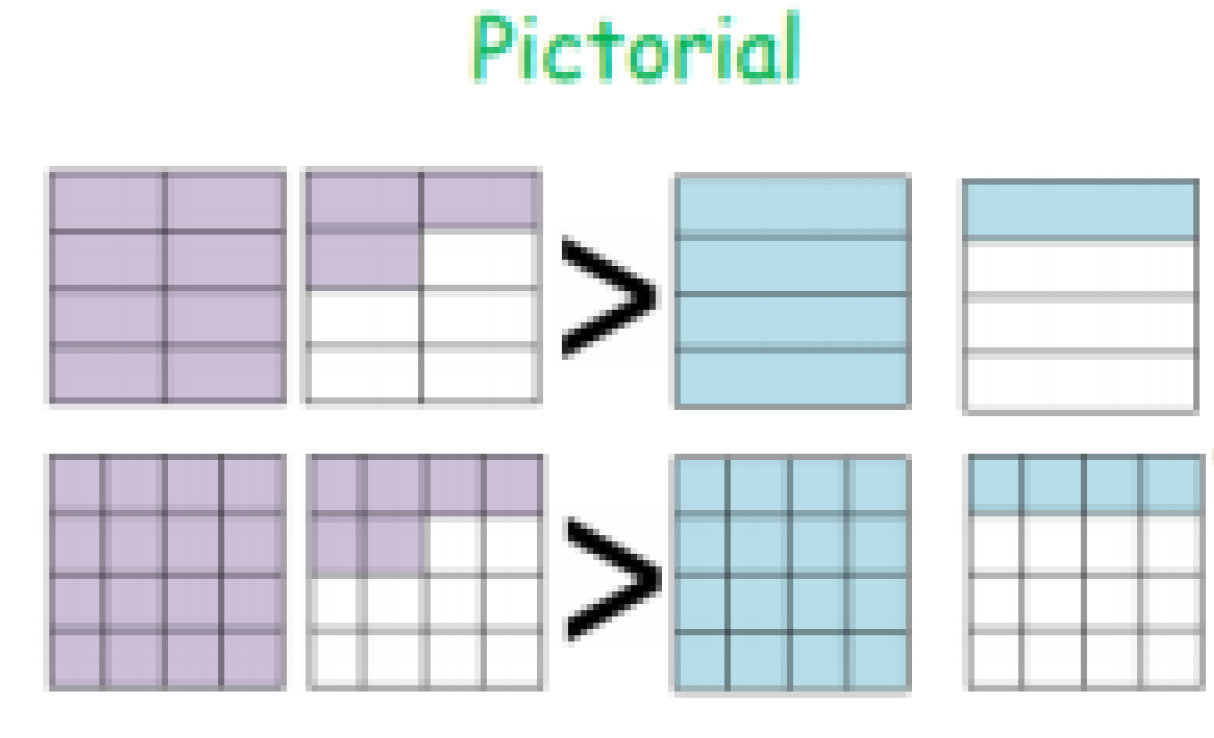
Children should understand the place value of tenths and hundredths and use this to align numbers with different numbers of decimal places.
Decimals used in the context of money and measures.
Key vocabulary: add, more, plus, and, make, altogether, total, equal to, equals, double, most, count on, number line, sum, tens, units, partition,
plus, addition, column, tens boundary, hundreds boundary, increase, exchange, vertical, thousands, hundreds, digits, inverse & decimal places, decimal point, tenths, hundredths, thousandths
Key skills for addition at Y5:
Add numbers mentally with increasingly large numbers, using and practising a range of mental strategies i.e. add the nearest multiple of 10, 100, 100 and adjust; use near doubles, inverse, partitioning and recombining; using number bonds.
Use rounding to check answers and accuracy.
Solve multi-step problems in contexts, deciding which operations and methods to use and why.
Read, write, order and compare numbers to at least 1 million and determine the value of each digit.
Round any number up to 1 000 000 to the nearest 10, 100, 1000, 10 000 and 100 000.
Add numbers with more than 4 digits using formal written method of column addition.
Year 6 Add numbers with up to 4-digits
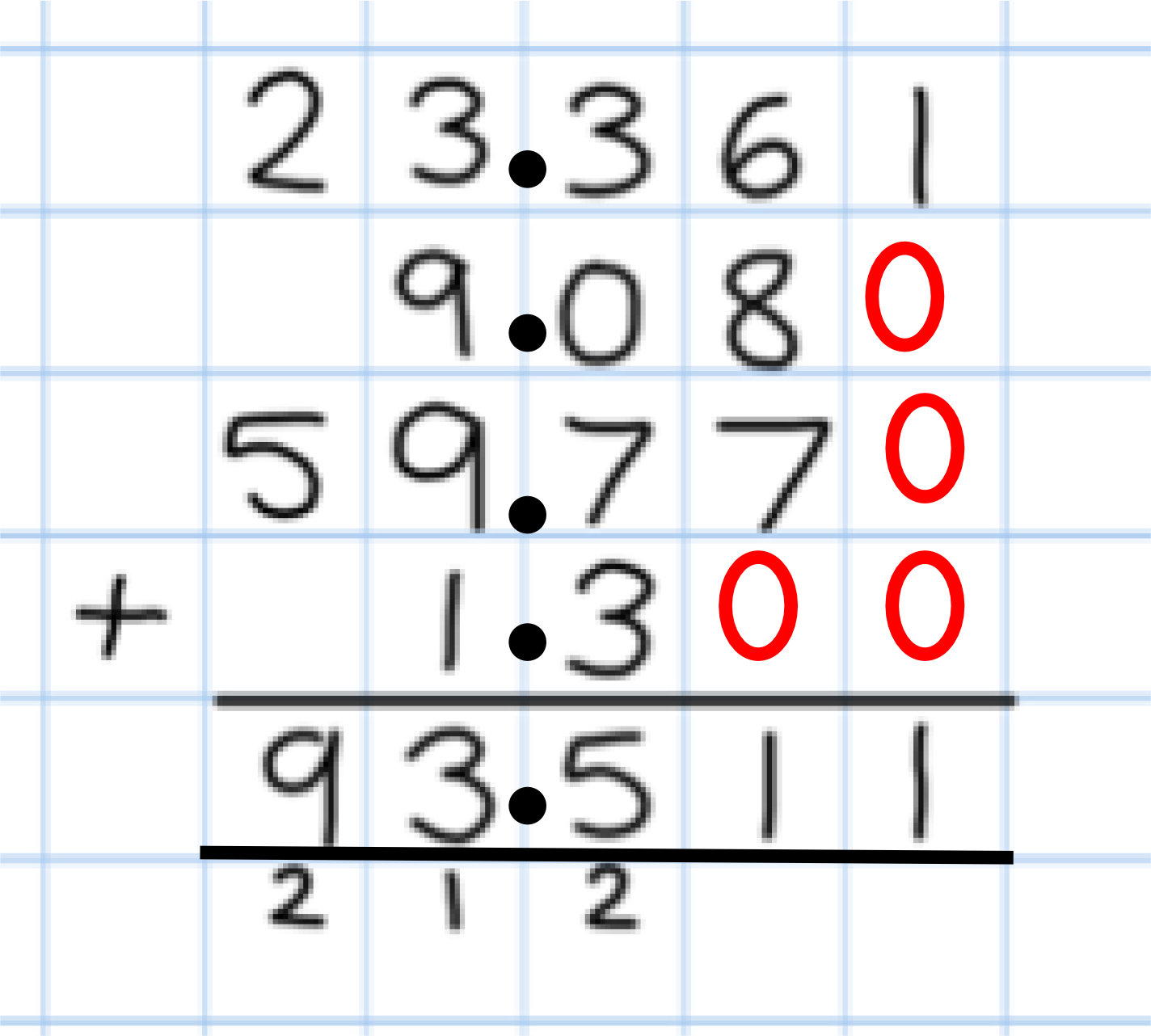
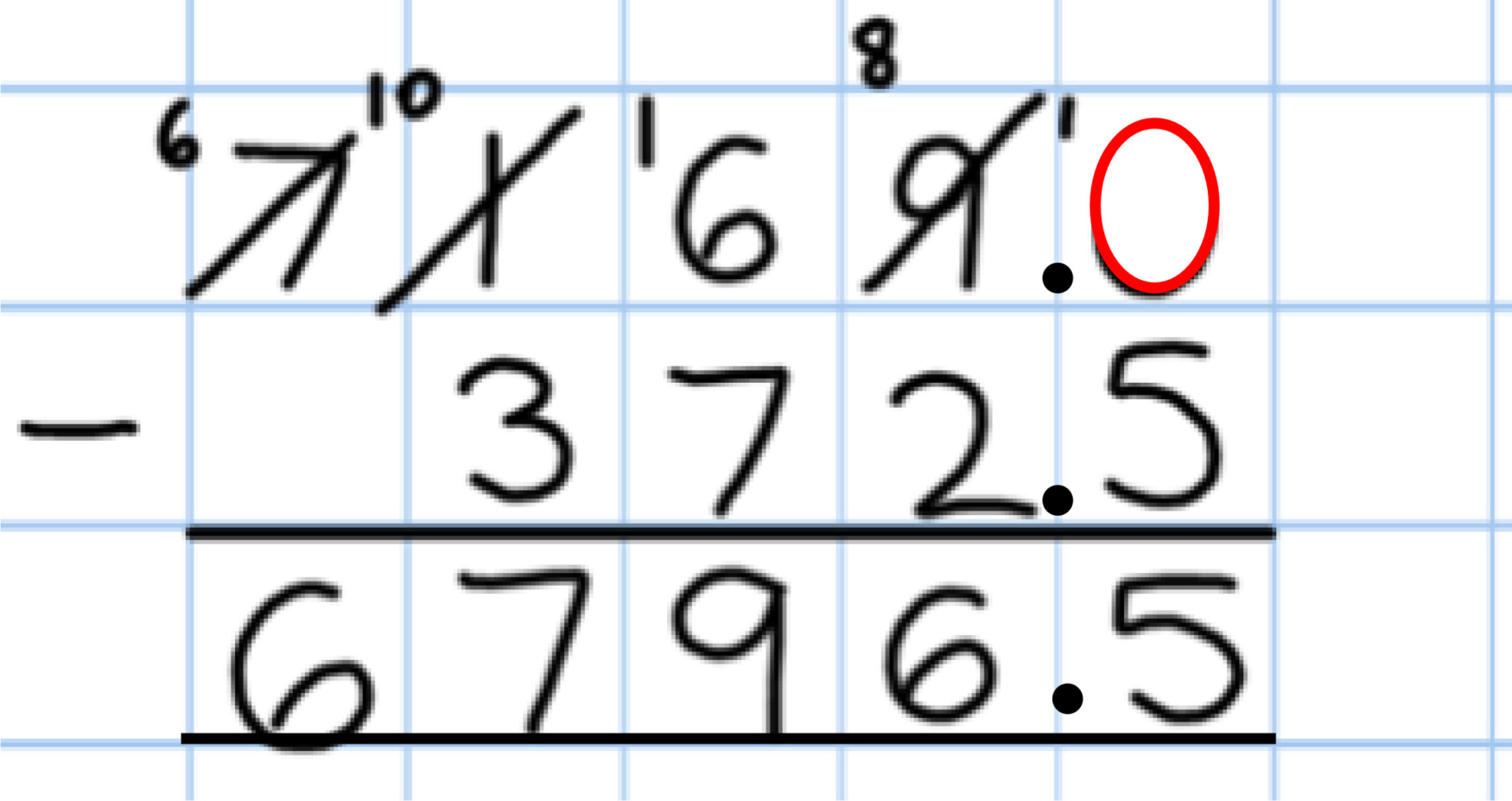
Adding several numbers with different numbers of decimal places (including money and measures): Tenths, hundredths and thousandths should be correctly aligned, with the decimal point lined up vertically including in the answer row.
Zeros should be added into any empty decimal places, to show there is no value to add.

Key vocabulary: add, more, plus, and, make, altogether, total, equal to, equals, double, most, count on, number line, sum, tens, units, partition,
plus, addition, column, tens boundary, hundreds boundary, increase, exchange, vertical, thousands, hundreds, digits, inverse, decimal places, decimal point, tenths, hundredths, thousandths
Key skills for addition at Y6:
Perform mental calculations, including with mixed operations and large numbers, using and practising a range of mental strategies.
Solve multi-step problems in context, deciding which operations and methods to use and why.
Use estimation to check answers to calculations and determine, in the context of a problem, levels of accuracy.
Read, write, order and compare numbers up to 10 million and determine the value of each digit.
Round any whole number to a required degree of accuracy.
Pupils understand how to add mentally with larger numbers and calculations of increasing complexity.